Question

Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt \(\widehat{POM}=\alpha;OM=R\left(0\le\alpha\le\dfrac{\pi}{3};R>0\right)\)

Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (H.63)

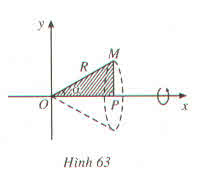
a) Tính thể tích của V theo \(\alpha\) và R

b) Tìm \(\alpha\) sao cho thể tích của V lớn nhất 

Answer 1

a) Hoành độ điểm P là :

x_p = OP = OM. cos α = R.cosα

Phương trình đường thẳng OM là y = tanα.x. Thể tích V của khối tròn xoay là:

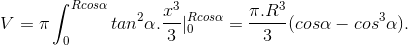
b) Đặt t = cosα => t ∈ 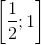. (vì α ∈ 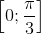), α = arccos t.

Ta có :

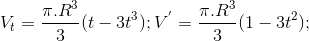
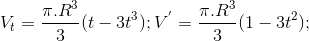
V' = 0 ⇔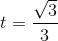

hoặc 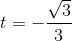(loại).

Từ đó suy ra V(t) lớn nhất ⇔ 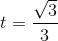, khi đó : .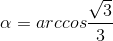