Bài 3: Ứng dụng của tích phân trong hình học
Các câu hỏi tương tự
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y=x mũ 2, trục hoành. Thể tích khối tròn xoay tạo thành khi quay hình (H) quanh trục ox bằng
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi :
a) y2-x^2;y1, quanh trục Ox
b) y2x-x^2;yx, quanh trục Ox
c) yleft(2x+1right)^{dfrac{1}{3}};x0;y3, quanh trục Oy
d) yx^2+1;x0 và tiếp tuyến với yx^2+1 tại điểm left(1;2right), quanh trục Ox
e) yln x;y0;xe, quanh trục Oy
Đọc tiếp
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi :
a) \(y=2-x^2;y=1\), quanh trục Ox
b) \(y=2x-x^2;y=x\), quanh trục Ox
c) \(y=\left(2x+1\right)^{\dfrac{1}{3}};x=0;y=3\), quanh trục Oy
d) \(y=x^2+1;x=0\) và tiếp tuyến với \(y=x^2+1\) tại điểm \(\left(1;2\right)\), quanh trục Ox
e) \(y=\ln x;y=0;x=e\), quanh trục Oy
Cho mặt phẳng (H) giới hạn bởi đồ thị hàm số y=x mũ 3 -x, trục hoành và hai đường thẳng x=0,x=1.Thể tích khối tròn xoay tạo thànhkhi quay hình (H) quanh trục ox bằng
Pham Trong Bach 12 tháng 7 2019 lúc 7:18 Tìm thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường y = 2-x và y = -x xung quanh trục Ox.
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt widehat{POM}alpha;OMRleft(0lealphaledfrac{pi}{3};R0right)
Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (H.63)
a) Tính thể tích của V theo alpha và R
b) Tìm alpha sao cho thể tích của V lớn nhất
Đọc tiếp
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt \(\widehat{POM}=\alpha;OM=R\left(0\le\alpha\le\dfrac{\pi}{3};R>0\right)\)
Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (H.63)
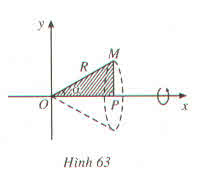
a) Tính thể tích của V theo \(\alpha\) và R
b) Tìm \(\alpha\) sao cho thể tích của V lớn nhất
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường ydfrac{1}{x};y0;x1;xa (a1)
Gọi thể tích đó là Vleft(aright). Xác định thể tích của vật thể khi arightarrow+infty (tức là limlimits_{arightarrow+infty}Vleft(aright)
Đọc tiếp
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đường \(y=\dfrac{1}{x};y=0;x=1;x=a\) (\(a>1\))
Gọi thể tích đó là \(V\left(a\right)\). Xác định thể tích của vật thể khi \(a\rightarrow+\infty\) (tức là \(\lim\limits_{a\rightarrow+\infty}V\left(a\right)\)
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox :
a) \(y=1-x^2;y=0\)
b) \(y=\cos x;y=0;x=0;x=\pi\)
c) \(y=\tan x;y=0;x=0;x=\dfrac{\pi}{4}\)
Tính thể tích vật thể giới hạn bởi miền hình phẳng tạo bởi các đường y=x2 và y=4 khi quay quanh trục Ox
Tính thể tích vật thể :
a) Có đáy là một tam giác cho bởi \(y=x;y=0;x=1\).Mỗi thiết diện vuông góc với trục Ox là một hình vuông
b) Có đáy là một hình tròn giới hạn bởi \(x^2+y^2=1\). Mỗi thiết diện vuông góc với trục Ox là một hình vuông




