Gọi G là trọng tâm tam giác ABC

\(\vec{MA}.\vec{MB}+\vec{MB}.\vec{MC}+\vec{MC}.\vec{MA}\)

\(=\dfrac{1}{2}\left(\vec{MA}+\vec{MB}+\vec{MC}\right)^2-\dfrac{1}{2}\left(MA^2+MB^2+MC^2\right)\)

\(\ge-\dfrac{1}{2}\left(MA^2+MB^2+MC^2\right)\)

\(=-\dfrac{1}{2}\left[\left(\vec{MG}+\vec{GA}\right)^2+\left(\vec{MG}+\vec{GB}\right)^2+\left(\vec{MG}+\vec{GC}\right)^2\right]\)

\(=-\dfrac{1}{2}\left[3MG^2+2\vec{MG}\left(\vec{GA}+\vec{GB}+\vec{GC}\right)+GA^2+GB^2+GC^2\right]\)

\(\ge-\dfrac{1}{2}\left(GA^2+GB^2+GC^2\right)\)

\(min=-\dfrac{1}{2}\left(GA^2+GB^2+GC^2\right)\Leftrightarrow M\equiv G\)

a. Xem lại đề bài, trị tuyệt đối đầu tiên 2 biểu thức MC trừ đi nhau thấy ko đúng

b. Gọi D là trung điểm AB, E là trung điểm BC

\(\Rightarrow\) DE là đường trung bình tam giác ABC

\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{AC}\) \(\Rightarrow\overrightarrow{AC}=2\overrightarrow{DE}\)

Ta có:

\(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{AC}\Leftrightarrow2\overrightarrow{MD}=2\overrightarrow{DE}\) (do D là trung điểm AB nên \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MD}\))

\(\Rightarrow\overrightarrow{MD}=\overrightarrow{DE}\Rightarrow D\) là trung điểm ME

\(\Rightarrow\) M là điểm đối xứng E qua D

Chọn C.

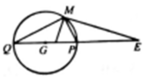
Gọi G là trọng tâm tam giác ABC và E là điểm thỏa mãn  E A   →   + 2 E B   → - E C → = 0

(điểm E như thế luôn tồn tại duy nhất). Khi đó đẳng thức trên tương đương với 3 M G → = M E →  hay 3 M G = M E . Trên đường thẳng GE ta lấy 2 điểm P, Q thỏa mãn 3 P G = P E = 3 Q G = Q E . Khi đó quỹ tích điểm M thỏa mãn yêu cầu là đường tròn đường kính PQ.

a: Xét ΔMAB co MA<AB+BM

b: MA<AB+BM

=>MA+MC<AB+BM+MC

=>MA+MC<AB+BC

Đề thiếu hay sao ấy b

ko bt nx bn ak

MA+MC= MA-MB

<=> 2 MI=BA

=> MI=BA/2

=> I thuộc đường tròn I bán kính AB/2

nãy mk quên giải thik: 

a, gọi I la trung điểm của AC=> MA+MC=2MI

hok tốt

b, 2MA+MB=4MB-MC

gọi I: 2OA+IB=0

gọi J: 4JB-JC=0

có: 

3MI=3MJ

MI=MJ

=> M thuộc đường trung trục của IJ