Xét ΔADF và ΔCBE có

AD=CB

\(\widehat{ADF}=\widehat{CBE}\)

DF=BE

Do đó: ΔADF=ΔCBE

=>AF=CE

Xét ΔABE và ΔCDF có

AB=CD

\(\widehat{ABE}=\widehat{CDF}\)

BE=DF

Do đó: ΔABE=ΔCDF

=>AE=CF

Xét tứ giác AECF có

AE=CF

AF=CE

Do đó: AECF là hình bình hành

a: Xét ΔMEA và ΔMCB có

góc EMA=góc CMB

MA=MB

góc MEA=góc MCB

=>ΔMEA=ΔMCB

=>ME=MC

=>M là trung điểm của CE

Xét tứ giác AEBC có

M là trung điểm chung của AB và EC

=>AEBC là hbh

b: Để AEBC là hình chữ nhật thì góc EAC=90 độ

=>góc DAC=90 độ

=>góc ACD+góc D=90 độ

mà góc ACD=1/2*góc D

nên góc D=2/3*90=60 độ

=>góc B=60 độ

góc BAD=góc BCD=180-60=120 độ

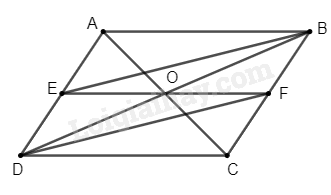
a) Vì \(ABCD\) là hình bình hành (gt)

Suy ra \(AD = BC\); \(AD\) // \(BC\)

Mà \(E\), \(F\) là trung điểm của \(AD\), \(BC\) (gt)

Suy ra \(AE = ED = BF = FC\)

Xét tứ giác \(EBFD\) ta có:

\(ED = FB\) (cmt)

\(ED\) // \(BF\) (do \(AD\) // \(BC\))

Suy ra \(EDFB\) là hình bình hành

b) Vì \(ABCD\) là hình bình hành (gt)

Suy ra \(O\) là trung điểm của \(AC\) và \(BD\)

Mà \(DEBF\) là hình bình hành (gt)

Suy ra \(O\) cũng là trung điểm của \(EF\)

Suy ra \(E\), \(O\), \(F\) thẳng hàng

Xét tứ giác DEBF có 

DE//BF

DE=BF

Do đó: DEBF là hình bình hành

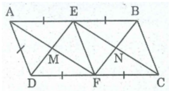
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF

ME = 1/2 DE (tính chất hình thoi)

MF = 1/2 AF (tính chất hình thoi)

Suy ra: DE = AF

⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)

⇒ ∠ A = 90 0  ⇒ Hình bình hành ABCD là hình chữ nhật.

Ngược lại: ABCD là hình chữ nhật ⇒  ∠ A =  90 0

Hình thoi AEFD có ∠ A =  90 0  nên AEFD là hình vuông

⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)

Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)

Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.

ABCD là hbh

=>O là trung điểm chung của AC và BD

OE+EA=OA

OF+FC=OC

mà OA=OC và EA=FC

nên OE=OF

=>O là trung điểm của EF

Xét tứ giác BEDF có

O là trung điểm chung của BD và EF

=>BEDF là hbh