đường thẳng d đi qua điểm M(1;2) và song song với đường thẳng 2x+3y-12=0 có PTTQ là ???? giúp mình cái

Những câu hỏi liên quan
Ở Hình 9 có ba đường thẳng được đánh số (1), (2), (3), (4) và ba điểm M, N, PHãy xác định đường thẳng nào là a, b, c, d, biết:- Đường thẳng a đi qua điểm M;- Đường thăng b chứa điểm P;- Đường thẳng c đi qua điểm N nhưng không chứa điểm M;- Đường thẳng d không đi qua cả ba điểm M, N, P
Đọc tiếp
Ở Hình 9 có ba đường thẳng được đánh số (1), (2), (3), (4) và ba điểm M, N, P
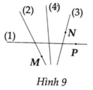
Hãy xác định đường thẳng nào là a, b, c, d, biết:
- Đường thẳng a đi qua điểm M;
- Đường thăng b chứa điểm P;
- Đường thẳng c đi qua điểm N nhưng không chứa điểm M;
- Đường thẳng d không đi qua cả ba điểm M, N, P
-Đường thẳng a là đường thẳng số 2
-Đường thẳng b là đường thẳng số 1
-Đường thẳng c là đường thẳng số 3
-Đường thẳng d là đường thẳng số 4
Đúng 0
Bình luận (0)
Cho đường thẳng y+(m+1).x+m(d)
a, Tìm giá trị của m để đường thẳng (d) đi qua điểm A(1;2)
b, Tìm giá trị của m để đường thẳng (d) song song với đườgn thẳng y=2x+3
c, Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi m
Cho đường thẳng y+(m+1).x+m(d)
a, Tìm giá trị của m để đường thẳng (d) đi qua điểm A(1;2)
b, Tìm giá trị của m để đường thẳng (d) song song với đườgn thẳng y=2x+3
c, Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi m
a: Thay x=1 và y=2 vào (d), ta được:
2m+1=2
hay m=1/2
Đúng 0
Bình luận (1)
Cho đường thẳng y+(m+1).x+m(d)
a, Tìm giá trị của m để đường thẳng (d) đi qua điểm A(1;2)
b, Tìm giá trị của m để đường thẳng (d) song song với đườgn thẳng y=2x+3
c, Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi m
b: Để hai đường song song thì m+1=2
hay m=1
Đúng 0
Bình luận (0)
Cho đường thẳng y+(m+1).x+m(d)
a, Tìm giá trị của m để đường thẳng (d) đi qua điểm A(1;2)
b, Tìm giá trị của m để đường thẳng (d) song song với đườgn thẳng y=2x+3
c, Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi m
: Cho đường thẳng: (d): y = (2m – 1)x + m – 2.
1) Tìm m để đường thẳng (d):
a. Đi qua điểm A(1; 6).
b. Song song với đường thẳng 2x + 3y – 5 = 0.
c. Vuông góc với đường thẳng x + 2y + 1 = 0.
2) Tìm điểm cố định mà (d) luôn đi qua với mọi m.
mn giảng giúp mình với, tại mình không hiểu ý ạ:( camon mn nhiều ạ
1.
\(a,\Leftrightarrow2m-1+m-2=6\Leftrightarrow3m=9\Leftrightarrow m=3\\ b,2x+3y-5=0\Leftrightarrow3y=-2x+5\Leftrightarrow y=-\dfrac{2}{3}x+\dfrac{5}{3}\)
Để \(\left(d\right)\text{//}y=-\dfrac{2}{3}x+\dfrac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2m-1=-\dfrac{2}{3}\\m-2\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{6}\\m\ne\dfrac{11}{3}\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{6}\)
\(c,x+2y+1=0\Leftrightarrow2y=-x-1\Leftrightarrow y=-\dfrac{1}{2}x-\dfrac{1}{2}\\ \left(d\right)\bot y=-\dfrac{1}{2}x-\dfrac{1}{2}\Leftrightarrow\left(-\dfrac{1}{2}\right)\left(2m-1\right)=-1\\ \Leftrightarrow\dfrac{1}{2}\left(2m-1\right)=1\Leftrightarrow m-\dfrac{1}{2}=1\Leftrightarrow m=\dfrac{3}{2}\)
2.
Gọi điểm cố định đó là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(2m-1\right)x_0+m-2\\ \Leftrightarrow2mx_0+m-x_0-2-y_0=0\\ \Leftrightarrow m\left(2x_0+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x_0=-1\\x_0+y_0+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{3}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho đường thẳng (d) có phương trình y =(2m-1)x-4m+5
a) Tìm m để (d) đi qua điểm M(-3; 1).
b) Chứng minh với mọi m đường thẳng (d) luôn đi qua 1 điểm cố định. Tìm tọa độ điểm đó.
a) (d) đi qua điểm \(M\left(-3;1\right)\Rightarrow1=\left(2m-1\right).\left(-3\right)-4m+5\)
\(\Rightarrow1=-6m+3-4m+5\Rightarrow1=-10m+8\Rightarrow10m=7\Rightarrow m=\dfrac{7}{10}\)
\(\Rightarrow y=\dfrac{2}{5}x+\dfrac{11}{5}\)
b) Gọi \(A\left(x_A;y_A\right)\) là điểm cố định mà (d) luôn đi qua
\(\Rightarrow y_A=\left(2m-1\right)x_A-4m+5\)
\(\Rightarrow2mx_A-x_A-4m+5-y_A=0\Rightarrow2m\left(x_A-2\right)-\left(x_A+y_A-5\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_A=2\\x_A+y_A-5=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_A=2\\y_A=3\end{matrix}\right.\Rightarrow A\left(2;3\right)\)
\(\Rightarrow\) (d) luôn đi qua điểm \(A\left(2;3\right)\) cố định
Đúng 2
Bình luận (0)
a) Thay x=-3 và y=1 vào (d), ta được:
\(\left(2m-1\right)\cdot\left(-3\right)-4m+5=1\)
\(\Leftrightarrow-6m+3-4m+5=1\)
\(\Leftrightarrow-10m=-7\)
hay \(m=\dfrac{7}{10}\)
Đúng 1
Bình luận (0)
cho đường thẳng (d) có phương trình y=(2m-1)x-4m+5
a) Tìm m để (d) đi qua điểm M(-3; 1).
b) Chứng minh với mọi m đường thẳng (d) luôn đi qua 1 điểm cố định. Tìm tọa độ điểm đó.
a.
Để d đi qua M \(\Rightarrow\) tọa độ M thỏa mãn pt d
\(\Rightarrow1=-3\left(2m-1\right)-4m+5\)
\(\Rightarrow m=\dfrac{7}{10}\)
b.
Giả sử tọa độ điểm cố định là \(A\left(x_0;y_0\right)\Rightarrow\) với mọi m ta luôn có:
\(y_0=\left(2m-1\right)x_0-4m+5\)
\(\Leftrightarrow2m\left(x_0-2\right)-\left(x_0+y_0-5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0-2=0\\x_0+y_0-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=3\end{matrix}\right.\)
Vậy với mọi m thì d luôn đi qua điểm cố định có tọa độ \(\left(2;3\right)\)
Đúng 5
Bình luận (0)
Quan sát hình bs 6

(A) đường thẳng d đi qua điểm T
(B) đường thẳng d đi qua hai điểm M và T
(C) đường thẳng d không đi qua điểm M và không đi qua điểm T
(D) đường thẳng d đi qua điểm M và không đi qua điểm T
Hãy chọn phương án đúng ?
Quan sát hình bs 6
(A) đường thẳng d đi qua điểm T
(B) đường thẳng d đi qua hai điểm M và T
(C) đường thẳng d không đi qua điểm M và không đi qua điểm T
(D) đường thẳng d đi qua điểm M và không đi qua điểm T
Hãy chọn phương án đúng ?
Đúng 0
Bình luận (0)
(D) đường thẳng d đi qua điểm M và không đi qua điểm T
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho đường thẳng d y = (m + 2) x + m Tìm m để d
a, song song với đường thẳng d1 : y = -2 x + 3
b ,vuông góc với đường thẳng d2 : y = 1 / 3 x + 1
C, đi qua điểm N( 1,3)
D, Tìm điểm cố định Mà D luôn đi qua với mọi m
\(a,d//d_1\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\m\ne3\end{matrix}\right.\Leftrightarrow m=-4\\ b,d\perp d_2\Leftrightarrow\dfrac{1}{3}\left(m+2\right)=-1\Leftrightarrow m+2=-3\Leftrightarrow m=-5\\ c,d.qua.N\left(1;3\right)\Leftrightarrow x=1;y=3\Leftrightarrow3=m+2+m\\ \Leftrightarrow2m=1\Leftrightarrow m=\dfrac{1}{2}\)
Đúng 2
Bình luận (1)
\(d,\) Gọi điểm đó là \(A\left(x_1;y_1\right)\)
\(\Leftrightarrow y_1=\left(m+2\right)x_1+m\\ \Leftrightarrow y_1-mx_1-2x_1-m=0\\ \Leftrightarrow-m\left(x_1+1\right)+y_1-2x_1=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_1+1=0\\y_1-2x_1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\y_1=-2\end{matrix}\right.\)
Vậy \(A\left(-1;-2\right)\) luôn đi qua D với mọi m
Đúng 2
Bình luận (0)




















