tìm m sao cho tồn tại một đường thẳng qua A(1;2) và cắt đồ thị y=(2x-2m+1)/(x-m-1) tại M,N phân biệt và tiếp tuyến tại M, N song song

Những câu hỏi liên quan
Cho hình bình hành ABCD.Qua A vẽ một đường thẳng sao cho đường thẳng này cắt đường chéo BD ở P và cắt DC,BC lần lượt ở M,N a, Chứng minh AP/AM+AP/AN=1 b,có tồn tại hệ thức AP/AM+AP/AN=1 hay không khi đường thẳng vẽ qua A cắt các tia CD,CB,DB lần lượt tại M,N,P? vì sao?
Bài 1 : Cho 2 điểm A và B nằm ngoài đường thẳng m. Qua A vẽ 50 đường thẳng trong đó có đường thằng đi qua B. Qua B vẽ 50 đường thẳng trong đó có đường thẳng đi qua A. Hỏi có ít nhất bao nhiêu giao điểm của đường thẳng m với các đường thẳng đã vẽ?Bài 2 : Cho 9 đường thẳng cắt nhau tại O tạo thành 1 số góc không có điểm chung. Chứng minh rằng trong các góc đó tồn tại một góc lớn hơn hoặc bằng 20 độ và tồn tại một hóc nhỏ hơn hoặc bằng 20 độ.Bài 3 : Qua điểm O nằm ngoài đường thẳng a vẽ một số đườn...
Đọc tiếp
Bài 1 : Cho 2 điểm A và B nằm ngoài đường thẳng m. Qua A vẽ 50 đường thẳng trong đó có đường thằng đi qua B. Qua B vẽ 50 đường thẳng trong đó có đường thẳng đi qua A. Hỏi có ít nhất bao nhiêu giao điểm của đường thẳng m với các đường thẳng đã vẽ?
Bài 2 : Cho 9 đường thẳng cắt nhau tại O tạo thành 1 số góc không có điểm chung. Chứng minh rằng trong các góc đó tồn tại một góc lớn hơn hoặc bằng 20 độ và tồn tại một hóc nhỏ hơn hoặc bằng 20 độ.
Bài 3 : Qua điểm O nằm ngoài đường thẳng a vẽ một số đường thẳng không phải tất cả điều cắt a. Những đường cắt a được 78 tam giác chung đỉnh O. Chứng minh rằng trong các đường thẳng đã vẽ qua O cũng có 2 đường thẳng cắt nhau theo một góc nhỏ hơn 13 độ.
Dùng phương pháp phản chứng
Cho điểm A (8; -1) và đường thẳng d: 2x - y - 7 = 0. Tồn tại đường thẳng \(\Delta\) đi qua O và cách A một khoảng lớn nhất. Hệ số góc của \(\Delta\) là ?
Đường thẳng d ở đây để làm gì nhỉ?
Theo định lý đường xiên - đường vuông góc ta có \(d\left(O;\Delta\right)\le OA\)
Dấu "=" xảy ra khi d vuông góc OA hay d nhận \(\overrightarrow{OA}=\left(8;-1\right)\) là 1 vtpt
Hệ số góc: \(k=-\dfrac{8}{-1}=8\)
Đúng 2
Bình luận (1)
1. Cho đường thẳng (d): y mx – 3. a) CMR: Đường thẳng (d) luôn đi qua một điểm cố định khi m thay đổi. b) Tìm giá trị của m để d cắt trục Ox; Oy lần lượt tại A; B sao cho số đo góc BAO 60. c) Tìm m để khoảng cách từ O đến d đạt giá trị lớn nhất.
Đọc tiếp
1. Cho đường thẳng (d): y = mx – 3.
a) CMR: Đường thẳng (d) luôn đi qua một điểm cố định khi m thay đổi.
b) Tìm giá trị của m để d cắt trục Ox; Oy lần lượt tại A; B sao cho số đo góc BAO = 60.
c) Tìm m để khoảng cách từ O đến d đạt giá trị lớn nhất.
a: Điểm mà (d) luôn đi qua là:
x=0 và y=m*0-3=-3
b: góc BAO=60 độ
=>góc tạo bởi (d) với trục Ox bằng60 độ
=>\(m=tan60=\sqrt{3}\)
c: y=mx-3
=>mx-y-3=0
\(d\left(O;d\right)=\dfrac{\left|0\cdot m+0\cdot\left(-1\right)-3\right|}{\sqrt{m^2+1}}=\dfrac{3}{\sqrt{m^2+1}}\)
Để d lớn nhất thì m^2+1 nhỏ nhất
=>m=0
Đúng 2
Bình luận (1)
Cho 2 điểm A (2; 0), B (4; 1) và đường thẳng d: y = x +3. Tồn tại điểm X thuộc đường thẳng d sao cho biểu thức \(\left|XA-XB\right|\) đạt Max. Tìm Max
Ta thấy A; B nằm cùng về 1 nửa mặt phẳng so với d
Theo BĐT tam giác: \(\left|XA-XB\right|\le AB\)
Đẳng thức xảy ra khi và chỉ khi X;A;B thẳng hàng hay X là giao điểm của AB và d
(Nếu ko cần tìm tọa độ điểm X mà chỉ cần tìm giá trị max thì tính độ dài AB là đủ)
\(\overrightarrow{AB}=\left(2;1\right)\Rightarrow\left|XA-XB\right|_{max}=AB=\sqrt{5}\)
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d:
x
1
-
2
a
+
a
t
y
-
2
+
2...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng d: x = 1 - 2 a + a t y = - 2 + 2 a + 1 - a t z = 1 + t . Biết rằng khi a thay đổi luôn tồn tại một mặt cầu cố định đi qua điểm M(1;1;1) và tiếp xúc với đường thẳng d. Tính bán kính R của mặt cầu đó.
A. R = 5 6
B. R = 6 3 5
C. R = 6 5
D. R = 5 3 6
Cho điểm A (1; 1), tồn tại điểm B thuộc đường thẳng d: 2x + 3y + 4 = 0 sao cho đường thẳng d và đường thẳng AB hợp với nhau một góc 45 độ. Biết điểm B có tung độ âm, hoành độ điểm B là ?
d nhận \(\left(2;3\right)\) là 1 vtpt nên nhận \(\overrightarrow{u}=\left(3;-2\right)\) là 1 vtcp
Do \(B\in d\) nên tọa độ có dạng: \(B\left(b;\dfrac{-2b-4}{3}\right)\Rightarrow\overrightarrow{AB}=\left(b-1;\dfrac{-2b-7}{3}\right)\)
\(cos45^0=\dfrac{\left|3.\left(b-1\right)+\dfrac{2\left(2b+7\right)}{3}\right|}{\sqrt{3^2+2^2}.\sqrt{\left(b-1\right)^2+\left(\dfrac{2b+7}{3}\right)^2}}=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow2\left(13b+5\right)^2=13\left(13b^2+10b+58\right)\)
\(\Leftrightarrow169b^2+130b-704=0\Rightarrow\left[{}\begin{matrix}b=-\dfrac{32}{13}\\b=\dfrac{22}{13}\Rightarrow y_B=-\dfrac{32}{13}< 0\left(loại\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
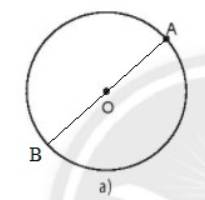
a) Lấy một điểm A bất kì trên đường tròn tâm O. Hãy tìm điểm B trên đường tròn sao cho O là trung điểm của đoạn thẳng AB (Hình 1a).
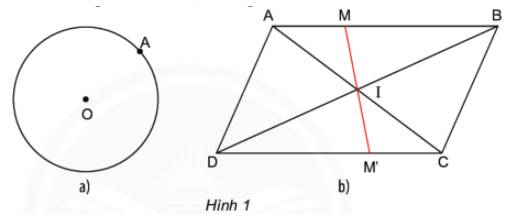
b) Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại I. Đường thẳng qua I cắt AB tại M và cắt CD tại M. Đo rồi so sánh độ dài IM và IM (Hình 1b).
a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
b) Độ dài IM = IM'.
Đúng 0
Bình luận (0)
Cho đường thẳng (d) y = (m+2)x + m (m là tham số)
a) Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi m
b) Tìm m để (d) cắt trục Ox, Oy tại A và B sao cho SAOB = \(\dfrac{1}{2}\left(đvdt\right)\)
a.
Giả sử điểm cố định mà (d) đi qua có tọa độ \(M\left(x_0;y_0\right)\)
Với mọi m, ta có:
\(y_0=\left(m+2\right)x_0+m\)
\(\Leftrightarrow m\left(x_0+1\right)+2x_0-y_0=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+1=0\\2x_0-y_0=0\end{matrix}\right.\) \(\Rightarrow M\left(-1;-2\right)\)
b. Để (d) cắt 2 trục tạo thành tam giác thì \(m\ne\left\{0;-2\right\}\)
Khi đó ta có: \(\left\{{}\begin{matrix}A\left(-\dfrac{m}{m+2};0\right)\\B\left(0;m\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|\dfrac{m}{m+2}\right|\\OB=\left|m\right|\end{matrix}\right.\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{m^2}{\left|m+2\right|}=1\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2=m+2\\m^2=-m-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)














