a: BC vuông góc SA

BC vuôg góc AB

=>BC vuông góc (SAB)

b: BI vuông góc SA
BI vuông góc AC

=>BI vuông góc (SAC)

Xét ΔHBA vuông tại H và ΔHAC vuông tại H có

góc HBA=góc HAC

=>ΔHBA đồng dạng với ΔHAC

=>HB/HA=HA/HC

=>HA^2=HB*HC

a: Xét ΔABC vuông tại A có sin C=AB/BC=3/5

=>cos C=căn 1-(3/5)^2=4/5

=>AC/BC=4/5

=>BC=20(cm)

\(AB=\sqrt{20^2-16^2}=12\left(cm\right)\)

ΔABC vuông tại A có AH là đường cao

nên CH*CB=CA^2

=>CH*20=16^2=256

=>CH=12,8(cm)

b: ΔHAB vuông tại H có HM là đường cao

nên AM*AB=AH^2

ΔHAC vuông tại H có HN là đường cao

nên AN*AC=AH^2

=>AM*AB=AN*AC

=>AM/AC=AN/AB

Xét ΔAMN vuông tại A và ΔACB vuông tại A có

AM/AC=AN/AB

Do đó: ΔAMN đồng dạng với ΔACB

Xét ΔAHB vuông tại H có HE là đường cao

nên AE*AB=AH^2

Xét ΔAHC vuông tại H có HD là đường cao

nên AD*AC=AH^2

=>AE*AB=AD*AC
=>AE/AC=AD/AB

mà góc DAE chung

nên ΔAED đồng dạng với ΔACB

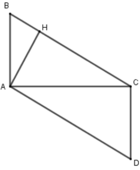
Xét ΔABC và ΔCDA có:

AB = CD (t/c)

AC chung

BAC = DCA = 90 ∘

Suy ra ΔABC = ΔCDA (c-g-c) nên D đúng.

Ta có: S A B C = 1 2 AH.BC = 1 2 AB.AC => AH.BC = AB.AC  ⇒ A H A B = A C B C

Xét ΔABC và ΔHAC có:

CAH = ABC (cùng phụ góc C)

A H A B = A C B C (cmt)

Suy ra ΔABC ~ ΔHAC (c - g - c) nên A sai

Ngoài ra, ΔADC = ΔCBA và ΔCBA ~ ΔCAH hay ΔADC ~ ΔCAH nên B đúng

Từ  A H A B = A C B C   ⇒ A H B C = A B B C

Xét ΔABH và ΔCBA có:

Chung B

=> ΔABH ~ ΔCBA (c-g-c)

Mà ΔADC = ΔCBA nên ΔABH ~ ΔADC hay C đúng

Vậy chỉ có A sai.

Đáp án: A

c: Xét ΔAHB vuông tại H có \(cosB=\dfrac{BH}{BA}\)

Xét ΔHMB vuông tại M có \(cosB=\dfrac{MB}{BH}\)

Xét ΔABC vuông tại A có \(\left\{{}\begin{matrix}cosB=\dfrac{BA}{BC}\\cosC=\dfrac{AC}{BC}\end{matrix}\right.\)

Xét ΔCKH vuông tại K có \(cosC=\dfrac{CK}{CH}\)

Xét ΔCHA vuông tại H có \(cosC=\dfrac{CH}{CA}\)

\(cos^3C=cosC\cdot cosC\cdot cosC\)

\(=\dfrac{CA}{CB}\cdot\dfrac{CK}{CH}\cdot\dfrac{CH}{CA}=\dfrac{CK}{CB}\)

=>\(CK=CB\cdot cos^3C\)

\(cos^3B=cosB\cdot cosB\cdot cosB\)

\(=\dfrac{BH}{BA}\cdot\dfrac{MB}{BH}\cdot\dfrac{BA}{BC}=\dfrac{MB}{BC}\)

=>\(MB=BC\cdot cos^3B\)

\(BM+CK\)

\(=BC\cdot cos^3B+BC\cdot cos^3C\)

\(=BC\left(cos^3B+cos^3C\right)\)