(d):mx-y+m=0 cắt đường cong (C):y=x^3-3x^2+4 tại ba điểm phân biệt lần lượt tại A B và C(-1;0) sao cho tam giác OAB có S=5 căn 5.Khi đó m là

Những câu hỏi liên quan
Cho hàm số
y
x
3
-
3
x
+
2
C
. Biết rằng đường thẳng
d
:
y
m
x
+
1
cắt
C
tại ba điểm phân biệt A, B, C. Tiếp tuyến tại ba điểm A, B, C của đồ thị cắt đồ thị
C
lần lượt tại các điểm A, B, C(tương ứng khác A, B, C). Biết rằng A, B, C thẳng hàng, tìm giá trị...
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 C . Biết rằng đường thẳng d : y = m x + 1 cắt C tại ba điểm phân biệt A, B, C. Tiếp tuyến tại ba điểm A, B, C của đồ thị cắt đồ thị C lần lượt tại các điểm A', B', C'(tương ứng khác A, B, C). Biết rằng A', B', C' thẳng hàng, tìm giá trị của tham số m để đường thẳng đi qua ba điểm A', B', C' vuông góc với đường thẳng ∆ : x + 2018 y - 2019 = 0
A. m = 1009 2
B. m = 1009 4
C. m = 2009 4
D. m = 2019 4
Chọn đáp án C

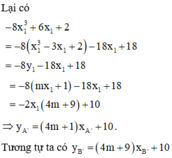
Do đó phương trình đường thẳng đi qua 3 điểm A’, B’, C’ là

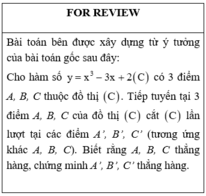
Đúng 0
Bình luận (0)
Cho parabol (P) y = x2 và đường thẳng (d) y = mx – m + 1 (m là tham số)
a) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt .
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho \(|x_A-x_B|< 3\) .
Biết xA và xB lần lượt là hoành độ giao điểm của hai điểm A, B.
cho (C) y=x^3+3x^2+mx-1 và d y= x+m+2 tìm m để d cắt (C) tại 3 điểm phân biệt ABC sao cho BC=4 , biết xA=1
Đường thẳng
d
:
y
x
-
3
cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi
d
1
,
d
2
lần lượt là khoảng cách từ A và B đến đường th...
Đọc tiếp
Đường thẳng d : y = x - 3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng D: x-y=0. Tính d = d 1 + d 2
A. d = 3 2
B. d = 3 2 2
C. d = 6
D. d = 2 2
Đường thẳng d:yx-3 cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng
△
:
x
-
y
0
Tính dd1+d A. B. C. d 6 D.
Đọc tiếp
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
Đáp án A
Phương trình hoành độ gioa điểm của d và (C) là
![]()
Suy ra ![]() suy ra
suy ra ![]() Dễ dàng tính được
Dễ dàng tính được ![]()
Đúng 0
Bình luận (0)
Cho hàm số y =\(\dfrac{2x-1}{x+2}\) (C) và đường thẳng d : y = mx - 2 . tìm m để (C) cắt d tại hai điểm phân biệt A , B sao cho I ( 2 ;0 ) là trung điểm của AB
cho p y=x^2 VÀ (d) y=mx+1(m khác 0)
a cm d cắt p tại 2 điểm phân biệt Avà B
b H VÀ K lần lượt là hình chiếu của A B trên Ox gọi I là giao điểm của d với oy
CM tam giác IHK vuông tại I với mọi giá trị của m khác 0
a) Phương trình hoành độ giao điểm của (d) và (P) là \(x^2=mx+1\Leftrightarrow x^2-mx-1=0\). (*)
Do ac < 0 nên phương trình luôn có 2 nghiệm phân biệt.
Do đó (d) cắt (P) tại 2 điểm phân biệt.
b) Do I có hoành độ là 0 nên có tung độ là 1. Do đó \(I\left(0;1\right)\).
Dễ thấy \(OI\perp HK\) và OI = 1.
Gọi \(x_1,x_2\) lần lượt là hoành độ của H và K.
Khi đó \(x_1,x_2\) là nghiệm của phương trình (*).
Theo hệ thức Viét ta có \(x_1x_2=-1\).
Ta có \(OK.OH=\left|x_1\right|.\left|x_2\right|=\left|x_1x_2\right|=1=OI^2\) nên tam giác IKH vuông tại I. (đpcm)
Đúng 3
Bình luận (0)
Cho parabol (P) y = x2 và đường thẳng (d) y = mx – m + 1 (m là tham số)
a) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt .
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho \(\left|x_A-x_B\right|< 3\) .
Biết xA và xB lần lượt là hoành độ giao điểm của hai điểm A, B.
a: Phương trình hoành độ giao điểm là: \(x^2-mx+m-1=0\)
\(\Delta=\left(-m\right)^2-4\cdot\left(m-1\right)=m^2-4m+4=\left(m-2\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì m-2<>0
hay m<>2
b: \(\left|x_A-x_B\right|< 3\)
\(\Leftrightarrow\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}< 3\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2< 9\)
\(\Leftrightarrow m^2-4\left(m-1\right)< 9\)
\(\Leftrightarrow\left(m-2\right)^2-3< 0\)
=>(m+1)(m-5)<0
=>-1<m<5
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đường thẳng ymx-m+1 cắt đồ thị của hàm số yx^3-3x^2+x+2 tại 3 điểm A, B, C phân biệt sao cho ABBCA. minleft(-infty;0right)cup[4;+infty)B. min RC. minleft(-dfrac{5}{4};+inftyright)D. minleft(-2;+inftyright)
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng \(y=mx-m+1\) cắt đồ thị của hàm số \(y=x^3-3x^2+x+2\) tại 3 điểm A, B, C phân biệt sao cho AB=BC
A. \(m\in\left(-\infty;0\right)\cup[4;+\infty)\)
B. \(m\in R\)
C. \(m\in\left(-\dfrac{5}{4};+\infty\right)\)
D. \(m\in\left(-2;+\infty\right)\)
















