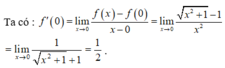Cho x>0; y>0 và x+y=1. Tìm MIN của \(M=\left(1-\frac{1}{x^2}\right)\left(1-\frac{1}{y^2}\right)\)

Những câu hỏi liên quan
Bài 1: Cho A= x(x-4). Với giá trị nào của x thì: A=0; A<0; A>0
Bài 2: Cho B= (x-3) : x (x khác 0). Với giá trị nào của x thì: B=0 ; B<0; B>0
tìm Timf Tìm tìm các số nguyên x và y sao cho(x-3) x (x+y) = 7các số nguyên x và y sao cho (x-3)(x+y)=7
Đề đây ạ:
Tìm các số nguyên x và y sao cho (x-3)(x+y)=7
123456789 x 0 x 0 x 0 x 0 x 0 = ?
Nhanh nhất mình tik cho, nhớ tik mình nhé
Giải
Vì a x 0 = 0
=> 123456789 x 0 x 0 x 0 x 0 x 0 = 0
Đúng 0
Bình luận (0)
123456789x0x0x0x0x0
=0
Chúc bạn học giỏi nha!!!
K mik mik k lại
Đúng 0
Bình luận (0)
123456789 x 0 x 0 x 0 x 0 x0 = 0 ( vì số nào nhân với 0 thì cũng bằng 0 )
k nha ^_-
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hàm số fleft( x right) left{ begin{array}{l} - 1,,,x 00,,,x 01,,,x 0end{array} right.Hàm số fleft( x right) có đồ thị ở Hình 6.a) Xét dãy số left( {{u_n}} right) sao cho {u_n} 0 và lim {u_n} 0. Xác định fleft( {{u_n}} right) và tìm lim fleft( {{u_n}} right).b) Xét dãy số left( {{v_n}} right) sao cho {v_n} 0 và lim {v_n} 0. Xác định fleft( {{v_n}} right) và tìm lim fleft( {{v_n}} right).
Đọc tiếp
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 1,\,\,x < 0\\0,\,\,x = 0\\1,\,\,x > 0\end{array} \right.\)
Hàm số \(f\left( x \right)\) có đồ thị ở Hình 6.
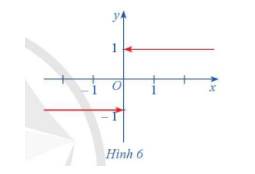
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Xác định \(f\left( {{u_n}} \right)\) và tìm \(\lim f\left( {{u_n}} \right).\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Xác định \(f\left( {{v_n}} \right)\) và tìm \(\lim f\left( {{v_n}} \right).\)
a) Xét dãy số \(\left( {{u_n}} \right)\) sao cho \({u_n} < 0\) và \(\lim {u_n} = 0.\) Khi đó \(f\left( {{u_n}} \right) = - 1\) và \(\lim f\left( {{u_n}} \right) = - 1.\)
b) Xét dãy số \(\left( {{v_n}} \right)\) sao cho \({v_n} > 0\) và \(\lim {v_n} = 0.\) Khi đó \(f\left( {{v_n}} \right) = 1\) và \(\lim f\left( {{v_n}} \right) = 1.\)
Đúng 0
Bình luận (0)
cho hpt x - 3y =0, (a - 1)x - 3y =2 (a là tham số)
tìm a để hpt có nghiệm (x,y) sao cho x>0, y>0
\(\left\{{}\begin{matrix}x-3y=0\\\left(a-1\right)x-3y=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-3y=0\\\left(a-2\right)x=2\end{matrix}\right.\)
Với \(a=2\) hệ vô nghiệm (ktm)
Với \(a\ne2\) hệ có nghiệm duy nhất: \(\left\{{}\begin{matrix}x=\dfrac{2}{a-2}\\y=\dfrac{x}{3}=\dfrac{2}{3\left(a-2\right)}\end{matrix}\right.\)
Để x>0; y>0
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2}{a-2}>0\\\dfrac{2}{3\left(a-2\right)}>0\end{matrix}\right.\) \(\Rightarrow a-2>0\Rightarrow a>2\)
Đúng 0
Bình luận (0)
cho x thuoc z mà x>0.tim x sao cho x.(-x)>0
Ta có x. (-x)=x.x.(-1)=-x^2>0
==> x^2<0 (vì âm của nó là dương) (1)
mà x>0==>x^2>0 (2)
Từ (1) và (2) ==> mâu thuẫn
Vậy x thuộc rỗng
Đúng 0
Bình luận (0)
cho x thuoc z mà x>0.tim x sao cho x.(-x)< 0
trong câu hỏi tương tự hay trên google đều không có đâu các bạn ạ
Đúng 0
Bình luận (0)
Cho các đa thức f(x),�(�), g(x)�(�) và h(x).ℎ(�). Xét các tập hợp X{x∈R|f(x)0},�{�∈�|�(�)0}, Y{x∈R|g(x)0},�{�∈�|�(�)0}, Z{x∈R|h(x)0}�{�∈�|ℎ(�)0} và T{x∈R|f2(x)+|g(x)|+√h(x)≤0}.�{�∈�|�2(�)+|�(�)|+ℎ(�)≤0}. Trong các mệnh đề dưới đây, mệnh đề nào đúng ?A. TX∪Y∪Z.��∪�∪�.B. TX∩Y∩Z.��∩�∩�.C. TX
Đọc tiếp
Cho các đa thức và Xét các tập hợp và Trong các mệnh đề dưới đây, mệnh đề nào đúng ?
A.
B.
C.
a)Cho A=x(x-4).Với giá trị nào của x thì :A=0;A<0;A>0
b)Cho B\(\frac{x-3}{x}\left(x\ne0\right)\).Với giá trị nào của x thì:B=0;B<0;B>
a)
Với A=0
\(\Rightarrow x\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=4\end{cases}}}\)
với A<0
\(\Rightarrow x\left(x-4\right)< 0\)
\(th1\orbr{\begin{cases}x< 0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x>4\end{cases}\Leftrightarrow4< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x>0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x< 4\end{cases}\Leftrightarrow0< x< 4\left(tm\right)}\)
\(\Leftrightarrow0< x< 4\Leftrightarrow x\in\left\{1;2;3\right\}\)
Với A>0
\(\Rightarrow x\left(x-4\right)>0\)
\(th1\orbr{\begin{cases}x>0\\x-4>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>0\\x>4\end{cases}}\Leftrightarrow x>4\)
\(th2\orbr{\begin{cases}x< 0\\x-4< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 0\\x< 4\end{cases}}\Leftrightarrow x< 0\)
b)
Với B=0
\(\Rightarrow\frac{x-3}{x}=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\Rightarrow x=3\\x=0\left(l\right)\end{cases}}\)
vậy x=3 thì B = 0
Với B < 0
\(\Rightarrow\frac{x-3}{x}< 0\)
\(th1\orbr{\begin{cases}x-3>0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x< 0\end{cases}\Leftrightarrow3< x< 0\left(vl\right)}\)
\(th2\orbr{\begin{cases}x-3< 0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x>0\end{cases}\Leftrightarrow0< x< 3\left(tm\right)\Leftrightarrow x\in\left\{1;2\right\}}\)
Với B > 0
\(th1\orbr{\begin{cases}x-3>0\\x>0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x>3\\x>0\end{cases}\Leftrightarrow x>3}\)
\(th2\orbr{\begin{cases}x-3< 0\\x< 0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 0\end{cases}\Leftrightarrow x< 0}\)
Cho hàm số f(x) xác định bởi
f
(
x
)
x
2
+
1
-
x
x
(
x...
Đọc tiếp
Cho hàm số f(x) xác định bởi f ( x ) = x 2 + 1 - x x ( x ≠ 0 ) 0 ( x = 0 ) . Giá trị f’(0) bằng:
A. 0
B. 1
C. 1/2.
D. Không tồn tại.