Tìm m để hệ phương trình { 3x - y = 5
{ 2x + my = 3m - 4
có nghiệm (x ; y) thỏa mãn 2x + 3y = 7

Những câu hỏi liên quan
Cho hệ phương trình: \(\left\{{}\begin{matrix}x+my=3m\\mx-y=m^2-2\end{matrix}\right.\)
Tìm m để hệ phương trình có nghiệm (x,y) thỏa mãn x2 - 2x - y > 0
Hệ \(\Leftrightarrow\left\{{}\begin{matrix}x=3m-my\\mx-y=m^2-2\end{matrix}\right.\)
\(\Rightarrow m\left(3m-my\right)-y=m^2-2\)
\(\Leftrightarrow2m^2+2=y\left(1+m^2\right)\)
\(\Leftrightarrow y=\dfrac{2m^2+2}{1+m^2}=2\)
\(\Rightarrow x=3m-2m=m\)
Có \(x^2-2x-y>0\Leftrightarrow m^2-2m-2>0\)
\(\Leftrightarrow\left(m-1-\sqrt{3}\right)\left(m-1+\sqrt{3}\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1+\sqrt{3}\\m< 1-\sqrt{3}\end{matrix}\right.\)
Vậy...
Đúng 2
Bình luận (8)
1) {x^2+2x^2=3 {2x^2+3x^2=5 2) giải theo m {x+y=2m+1 {x-y=1 3)giải theo m {x +2y=3m+2 {2x+y=3m+2 4) cho hệ. {x+3y=4m+4 {2x+y=3m+3 Tìm m để hệ có nghiệm (x,y) thỏa mãn x+y=4 HỆ PHƯƠNG TRÌNH HẾT Ạ Giúp mik với nhé
4:
x+3y=4m+4 và 2x+y=3m+3
=>2x+6y=8m+8 và 2x+y=3m+3
=>5y=5m+5 và x+3y=4m+4
=>y=m+1 và x=4m+4-3m-3=m+1
x+y=4
=>m+1+m+1=4
=>2m+2=4
=>2m=2
=>m=1
3:
x+2y=3m+2 và 2x+y=3m+2
=>2x+4y=6m+4 và 2x+y=3m+2
=>3y=3m+2 và x+2y=3m+2
=>y=m+2/3 và x=3m+2-2m-4/3=m+2/3
Đúng 0
Bình luận (0)
Tìm quan hệ giữa S và P để hệ phương trình
x+y=S
xy=P
có nghiệm.
Hệ phương trình
x2y+xy2=2m
x+y=4
có nghiệm duy nhất khi m bằng:
Định m để hệ phương trình
x+y-4xy=2m
x2+y2-2xy=m+1
có nghiệm.
Cho hệ phương trình:
\(\hept{\begin{cases}2x+my=5\\3x-y=0\end{cases}}\)
a, Giải hệ phương trình khi m=0.
b, Tìm m để hệ có nghiệm duy nhất.
c, Tìm m để hệ phương trình có nghiệm x,y thỏa mãn: x - y = 1.
a) \(\hept{\begin{cases}2x+my=5\\3x-y=0\end{cases}\left(1\right)}\)
Thay m=0 vào (1) \(\Rightarrow\hept{\begin{cases}2x=5\\3x-y=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\\frac{5}{2}\cdot3=y\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{5}{2}\\y=\frac{15}{2}\end{cases}}}\)
Cho hệ phương trình: 2X +Y = 3m-2 ( m là tham số ) X - Y = 5 a) Giải hệ phương trình khi m = - 4 ; b) Tìm m để hệ phương trình có nghiệm (x; y) thỏa mãn: x + y = 13.
Cho hệ phương trình (m-1)x-my=3m-1 và 2x-y=m+5
a) Giải hệ phương trình với m=2
b) Tìm m để hệ phương trình có nghiệm (x;y) duy nhất thỏa mãn x2 - y2 <4
a)Với m=2 thì hpt trở thành:
x-2y=5
2x-y=7
<=>
2x-4y=10
2x-y=7
<=>
-3y=3
2x-y=7
<=>
y=-1
x=3
b)\(\int^{\left(m-1\right)x-my=3m-1}_{2x-y=m+5}\Leftrightarrow\int^{x=\frac{3m+my-1}{m-1}}_{\frac{6m+2my-2}{m-1}-y=m+5}\Leftrightarrow\int^{x=\frac{3m+my-1}{m-1}}_{m^2+2m+my+y+3=0}\)
*m2+2m+my+y+3=0
<=>y.(m+1)=-m2-2m-3
*Với m=-1 =>PT vô nghiệm
*Với m khác -1 =>PT có nghiệm là: \(y=\frac{-m^2-2m-3}{m+1}=-m-1-\frac{2}{m+1}\)
bí tiếp
Đúng 0
Bình luận (0)
Bài 1:Cho hệ
mx+y=3 (1)
9x+my=2m+3 (2)
Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn: 3x+2y=9
Bài 2:Cho hệ
mx+y= m^2
x+my=1 (m là tham số)
Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x+y>0
Cho hệ phương trình:
(m-1)x-my=3m-1
2x-y=m=5.
Tìm m để hệ phương trình có nghiệm duy nhất ( x, y) sao cho S=x2+y2 đạt giá trị nhỏ nhất
Tìm m để hệ phương trình:
{3x - y = 2m + 3
{x + 2y = 3m + 1
có nghiệm (x;y) thỏa mãn x^2 + y^2 = 5
\(HPT\Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m+6\\x+2y=3m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=7m+7\\x+2y=3m+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=m+1\\m+1+2y=3m+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m+1\\y=m\end{matrix}\right.\)
\(x^2+y^2=5\Leftrightarrow m^2+2m+1+m^2=5\\ \Leftrightarrow2m^2+2m-4=0\\ \Leftrightarrow m^2+m-2=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Đúng 3
Bình luận (0)














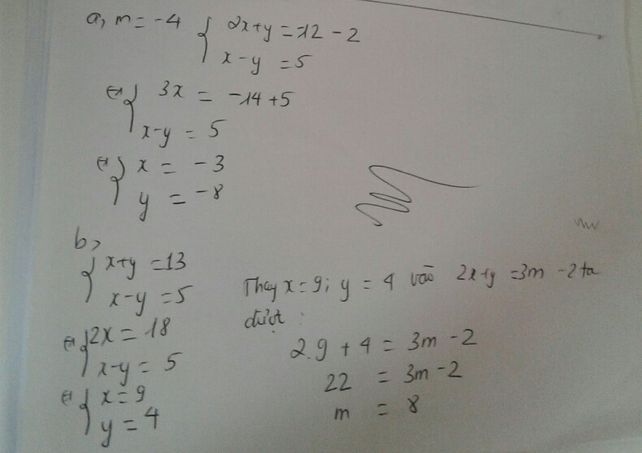 Bn tham khảo nhé!
Bn tham khảo nhé!







