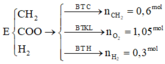
Với m,n∈Zm,n∈Z ; sao cho \(\dfrac{1}{m}\)+\(\dfrac{n}{6}\)=12. Số cặp giá trị (m;n)(m;n) thỏa mãn là

Những câu hỏi liên quan
Cho y(n+p)=z(p+m) trong đó x,y,z là 3 số khác nhau và khác 0 CMR: (m-n)/x(y-z)=(n-p)/y(z-x)=(p-m)/z(x-y).
giúp suli với các bn nekkkkkkkkkkkkk
chứng minh m.n.(m^2.n^2) chia hết cho 6 với mọi m;n thuộc Z
Ta có : m.n( m2.n2 )
= m.n [( m2 - 1 ) - ( n2 - 1)]
= m( m2 - 1 )n - mn( n2 - 1 )
= ( m - 1 )m( m + 1 )n - m( n - 1 )n( n + 1 )
Ta thấy: * ( m - 1) ; m và ( m + 1) là ba số nguyên liên tiếp
=> ( m - 1 )m( m + 1 ) chia hết cho 6
=> ( m - 1 )m ( m + 1 )n chia hết cho 6 (1)
* ( n - 1) ; n ; ( n + 1 ) là ba số nguyên liên tiếp
=> ( n - 1)n( n + 1 ) chia hết cho 6
=> m( n - 1 )n( n + 1 ) chia hết cho 6 (2)
Từ (1) và (2) suy ra : ( m - 1)m( m + 1)n - m( n - 1)n( n + 1 ) chia hết cho 6
Vậy m.n( m2.n2 ) chia hết cho 6 (đpcm)
Hok tốt !
Đúng 0
Bình luận (0)
Em kiểm tra lại đề và có thể tham khảo 1 cách giải ( lớp 7 có thể hiểu):
Câu hỏi của Luong Ngoc Quynh Nhu - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
thế m=n=1 t/m không??? mà c/m như thật vậy?? bạn: Nguyễn Ngọc Minh
Đúng 0
Bình luận (0)
các bạn giúp mình với
Tìm các số nguyên x, y, z biết:
x phần 10 = âm 7 phần y = z phần âm 24 = âm bốn phần 8
giúp mình với tối nay 7h mình đ hok ùi. huhu giúp mink với
1. cho phân số M=6n-1/3n+2 ( n thuộc Z )
a> tìm n thuộc z để M nhận giá trị nguyên
b> tìm số tự nhiên n để M có GTNN. Tìm giá trị đó
c> tìm n để M là phân số tối giản
a) Để M nhận giá trị nguyên thì \(6n-1⋮3n+2\)
\(\Leftrightarrow6n+4-5⋮3n+2\)
\(\Leftrightarrow2\left(3n+2\right)-5⋮3n+2\)
Do \(2\left(3n+2\right)⋮3n+2\) \(\Rightarrow5⋮3n+2\)
Do 3n+2 chia 3 dư 2, mà 5 chia hết cho 3n+2
\(\Rightarrow3n+2\in\left\{-1;5\right\}\)
\(\Leftrightarrow n\in\left\{-1;1\right\}\)
Vậy: n=-1 hoặc n=1
Đúng 0
Bình luận (0)
A=2n + 3 phần n (n thuộc Z)
a với giá trị nào của n thì A là phân số
b với giá trị nào của n thì A là số thuộc Z
\(A=\frac{2n+3}{n}=2+\frac{3}{n}\)
a) A là phân số <=> n khác Ư(3) <=> n khác (+-1; +-3)
b) A thuộc Z <=> n thuộc Ư(3) <=> n thuộc (+-1; +-3)
Đúng 0
Bình luận (0)
X, Y, Z là 3 axit cacboxylic đơn chức cùng dãy đồng đẳng (MX MY MZ), T là este tạo bởi X, Y, Z với 1 ancol no, ba chức, mạch hở E. Đốt cháy hoàn toàn 26,6 gam hỗn hợp M gồm X, Y, Z, T (trong đó Y, Z có cùng số mol) bằng lượng vừa đủ khí O2, thu được 22,4 lít CO2 (đktc) và 16,2 gam nước. Mặt khác, đun nóng 26,6 gam M với lượng dư dung dịch AgNO3/NH3. Sau khi phản ứng xảy ra hòa toàn, thu được 21,6 gam Ag. Mặt khác 13,3 gam M phản ứng hết với 400 ml dung...
Đọc tiếp
X, Y, Z là 3 axit cacboxylic đơn chức cùng dãy đồng đẳng (MX < MY < MZ), T là este tạo bởi X, Y, Z với 1 ancol no, ba chức, mạch hở E. Đốt cháy hoàn toàn 26,6 gam hỗn hợp M gồm X, Y, Z, T (trong đó Y, Z có cùng số mol) bằng lượng vừa đủ khí O2, thu được 22,4 lít CO2 (đktc) và 16,2 gam nước. Mặt khác, đun nóng 26,6 gam M với lượng dư dung dịch AgNO3/NH3. Sau khi phản ứng xảy ra hòa toàn, thu được 21,6 gam Ag. Mặt khác 13,3 gam M phản ứng hết với 400 ml dung dịch NaOH 1M và đun nóng, thu được dung dịch N. Cô cạn dung dịch N thu được m gam chất rắn khan. Giá trị của m gần nhất với
A. 38,04.
B. 16,74.
C. 25,10.
D. 24,74.
X, Y, Z là 3 axit cacboxylic đơn chức cùng dãy đồng đẳng (MX MY MZ), T là este tạo bởi X, Y, Z với 1 ancol no, ba chức, mạch hở E. Đốt cháy hoàn toàn 26,6 gam hỗn hợp M gồm X, Y, Z, T (trong đó Y, Z có cùng số mol) bằng lượng vừa đủ khí O2, thu được 22,4 lít CO2 (đktc) và 16,2 gam nước. Mặt khác, đun nóng 26,6 gam M với lượng dư dung dịch AgNO3/NH3. Sau khi phản ứng xảy ra hòa toàn, thu được 21,6 gam Ag. Mặt khác 13,3 gam M phản ứng hết với 400 ml dung...
Đọc tiếp
X, Y, Z là 3 axit cacboxylic đơn chức cùng dãy đồng đẳng (MX < MY < MZ), T là este tạo bởi X, Y, Z với 1 ancol no, ba chức, mạch hở E. Đốt cháy hoàn toàn 26,6 gam hỗn hợp M gồm X, Y, Z, T (trong đó Y, Z có cùng số mol) bằng lượng vừa đủ khí O2, thu được 22,4 lít CO2 (đktc) và 16,2 gam nước. Mặt khác, đun nóng 26,6 gam M với lượng dư dung dịch AgNO3/NH3. Sau khi phản ứng xảy ra hòa toàn, thu được 21,6 gam Ag. Mặt khác 13,3 gam M phản ứng hết với 400 ml dung dịch NaOH 1M và đun nóng, thu được dung dịch N. Cô cạn dung dịch N thu được m gam chất rắn khan. Giá trị của m gần nhất với
A. 38,04.
B. 16,74
C. 25,10.
D. 24,74.
Chọn D
Dồn chất:
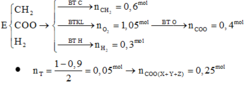
→ B T K L m = 26 , 6 + 0 , 8 . 40 - 0 , 05 . 92 - 18 . 0 , 25 2 = 24 , 75 g a m
·
Đúng 0
Bình luận (0)
5,6 lít hỗn hợp (Z) gồm O 2 và Cl 2 ở đktc. Tỉ khối của (Z) đối với khí H 2 là 29.
a. Tính % ( theo thể tích) mỗi khí trong hỗn hợp
b. Tính số mol mỗi khí trong hỗn hợp.
Ta có:
\(n_{hh}=\frac{5,6}{22,4}=0,25\left(mol\right)\)
Gọi \(\left\{{}\begin{matrix}n_{O2}:x\left(mol\right)\\n_{Cl2}:y\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow x+y=0,25\left(1\right)\)
\(\Rightarrow\frac{32x+71y}{x+y}=58\Rightarrow58x+58y=32x+71y\)
\(\Rightarrow26x=13y\) hay \(26x-13y=0\left(2\right)\)
\(\Rightarrow\frac{x}{y}=\frac{1}{2}\)
\(\left\{{}\begin{matrix}\%V_{O2}=\frac{1}{3}.100\%=33,33\%\\\%V_{Cl2}=100\%-33,33\%=66,67\%\end{matrix}\right.\)
b) \(\left(1\right)+\left(2\right)\Rightarrow\left\{{}\begin{matrix}x+y=0,25\\26x-13y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\frac{1}{12}\left(mol\right)\\y=\frac{1}{6}\left(mol\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) Chứng minh: M = n - 1 phần n - 2 ( n thuộc Z; n không bằng 2 ) là phân số tối giản.
b) Chứng minh: M = 2n + 1 phần n ( n thuộc Z; n không bằng 0 ) là phân số tối giản.
Giúp mình với ạ, sắp nộp bài rùi, bạn nào sớm mình sẽ tick cho!!!!!!