Biết rằng: sin4x + cos4x = m.cos4x + n ( trong đó m; n là các số hữu tỉ) . Tính S = 3m – n.
A. S = 0
B. S = -1
C. S = 1
D. S = 2
Biết rằng sin 4 x + cos 4 x = m . cos 4 x + n ( m , n ∈ ℚ ) . Tính tổng S = m + n
A. 7/4
B. 1
C. 2
D. 5/4
Biết rằng sin 4 x + c o s 4 x = m c o s 4 x + n m , n ∈ ℚ . Tính tổng S = m + n
A. S = 5 3
B. S = 1
C. S = 2
D. S = 5 4
Đáp án B
Ta có
sin 4 x + c o s 4 x = m c o s 4 x + n ⇔ sin 2 x + c o s 2 x − 2 sin 2 x . c o s 2 x = m c o s 4 x + n ⇔ 1 − 1 2 sin 2 2 x = m c o s 4 x + n ⇔ 1 − 1 − c o s 4 x 4 = m c o s 4 x + n ⇒ m = 1 4 n = 3 4 ⇒ S = 1
Câu 1 : Chứng minh rằng : 3 - 4sin2x = 4cos2x - 1Câu 2 : Chứng minh rằng : cos4x - sin4x = 2cos2x - 1 = 1 - 2sin2xCâu 3 : Chứng minh rằng : sin4x + cos4x = 1 - 2sin2xCos2x
1/ \(3-4\sin^2=4\cos^2x-1\Leftrightarrow4\left(\sin^2x+\cos^2x\right)-4=0\Leftrightarrow4.1-4=0\left(ld\right)\Rightarrow dpcm\)
2/ \(\cos^4x-\sin^4x=\left(\cos^2x+\sin^2x\right)\left(\cos^2x-\sin^2x\right)=\cos^2x-\left(1-\cos^2x\right)=2\cos^2x-1=\left(1-\sin^2x\right)-\sin^2x=1-2\sin^2x\)
3/ \(\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x.\cos^2x=1-2\sin^2x.\cos^2x\)
Biết \(\dfrac{cos4x+cos2x+1}{sin4x+sin2x}=m.cotx\). Tìm m?
Ý bạn là $m\cot 2x$?
Lời giải:
$\frac{\cos 4x+\cos 2x+1}{\sin 4x+\sin 2x}=\frac{\cos ^22x-\sin ^22x+\cos 2x+1}{2\sin 2x\cos 2x+\sin 2x}$
$=\frac{2\cos ^22x-1+\cos 2x+1}{\sin 2x(2\cos 2x+1)}$
$=\frac{2\cos ^22x+\cos 2x}{\sin 2x(2\cos 2x+1)}$
$=\frac{\cos 2x(2\cos 2x+1)}{\sin 2x(2\cos 2x+1)}$
$=\frac{\cos 2x}{\sin 2x}=\cot 2x$
$\Rightarrow m=1$
Cho phương trình: 4(sin4x + cos4x ) – 8(sin6x + cos6x) - 4sin24x = m trong đó m là tham số. Để phương trình là vô nghiệm, thì các giá trị thích hợp của m là:
![]()
![]()
![]()
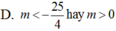

(1) trở thành 4t2 – 2t -6 – m = 0 (2); △ ' = 25 + 4 m .
Để (1) vô nghiệm, ta sẽ tìm m sao cho (1) có nghiệm rồi sau đó phủ định lại.
(1) có nghiệm thì (2) phải có nghiệm thoả t o ∈ - 1 ; 1
Nếu 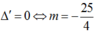 , (2) có nghiệm kép
, (2) có nghiệm kép 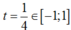 nên
nên ![]() thoả (1) có nghiệm.
thoả (1) có nghiệm.
Nếu ![]() , khi đó (2) phải có hai nghiệm phân biệt thoả
, khi đó (2) phải có hai nghiệm phân biệt thoả 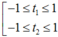
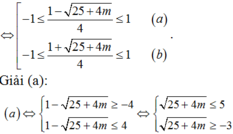
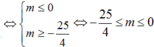
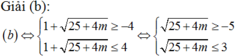
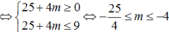

Chứng minh rằng f′(x) = 0 ∀x ∈ R , nếu: f ( x ) = 3 ( sin 4 x + cos 4 x ) − 2 ( sin 6 x + cos 6 x )
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0
sinx-cosx bằng 1 phần 2 tính M bằng sin4x cộng cos4x
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x.
A = 2( sin 4 x + cos 4 x + sin 2 x . cos 2 x ) 2 - ( sin 8 x + cos 8 x )
Ta có:
![]()
![]()
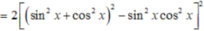

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy giá trị của biểu thức  không phụ thuộc vào x.
không phụ thuộc vào x.
Chưng minh phương trình sau luôn có nghiệm với mọi m :
sin4x +cos4x+msinx .cosx =1/2
PT\(\Leftrightarrow1-2sin^2x.cos^2x+m.sinx.cosx=\dfrac{1}{2}\)
\(\Leftrightarrow1-\dfrac{sin^22x}{2}+\dfrac{m}{2}\cdot sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow sin^22x-m.sin2x-1=0\left(\cdot\right)\)
Đặt \(t=sin2x\left(-1\le t\le1\right)\)
PT(*) trở thành: \(t^2-m.t-1=0\)
Để PT có nghiêm thì \(\Delta\ge0\Leftrightarrow m^2-4.1.\left(-1\right)\ge0\Leftrightarrow m^2+4\ge0\)
Dễ thấy \(m^2+4\ge0\left(\forall m\right)\)
Do đó PT (*) luôn có nghiệm với mọi m