Chọn A.
Ta có : sin4x + cos4x = ( sin2x + cos2x) 2- 2sin2x.cos2x = 1- 2( ½ .sin2x) 2
![]()
Do đó: m = ¼ và n = ¾
Và S = 0.
Chọn A.
Ta có : sin4x + cos4x = ( sin2x + cos2x) 2- 2sin2x.cos2x = 1- 2( ½ .sin2x) 2
![]()
Do đó: m = ¼ và n = ¾
Và S = 0.
Biết rằng sin6x + cos6x = mcos 4x + n ; Trong đó m và n là các số hữu tỉ. Tính S = 5m- 3n.
A. S = 1
B. S = - 1
C. S = 0
D. S = 2
Biết rằng đồ thị hàm số y = ax + b đi qua hai điểm M(-1; 3) và N(1; 2). Tính tổng S = a + b.
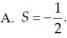
B. S = 3.
C. S = 2.
D. 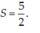
Biết rằng đồ thị hàm số y = ax + b đi qua hai điểm M(−1; 3) và N(1; 2). Tính tổng S = a + b.
A. S = - 1 2
B. S = 3
C. S = 2
D. S = 5 2
Biết phương trình 3 x + 1 − 3 x 2 + 7 x − 3 x − 1 = 0 có một nghiệm có dạng x = a + b c , trong đó a, b, c là các số nguyên tố. Tính S=a+b+c
A. S = 14
B. S = 21
C. S = 10
D. S = 12
Cho 2 số \(n,k\inℤ^+\) và S là tập hợp \(n\) điểm trên mặt phẳng thỏa mãn các điều kiện sau:
1. Không có 3 điểm nào trong S thẳng hàng.
2. Với mọi điểm P thuộc tập S, tồn tại ít nhất \(k\) điểm khác trong S cách đều P.
Chứng minh rằng \(k< \dfrac{1}{2}+\sqrt{2n}\)
Cho các số thực dương x,y thỏa mãn x+2y+3xy=3 . Biết rằng biểu thức P= x+y đạt giá trị nhỏ nhất bằng \(\frac{a\sqrt{b}-c}{3}\)
trong đó a,b,c là các số nguyên dương . Gọi S là tập hợp các giá trị của M= a+b+c , tính tổng bình phương các phần tử của S
Cho hình bình hành ABCD. Biết rằng \(\overrightarrow{BD}\) = m\(\overrightarrow{BA}\) +n\(\overrightarrow{BC}\) với m, n là các số thực. Tính giá trị của S = 20m +21n.
Cho bpt: (m-2)x^2 + 2(4-3m)x + 10m -11 ≤ 0 (1). Gọi S là tập hợp các số nguyên dương m để bpt đúng với mọi ∀x < -4. Tìm số phần tử của S.
Cho đường thẳng delta x-2y+1=0 và 2 điểm A(6;5), B(-4;1). Biết điểm P (a;b) thuộc đg thẳng delta thõa mản PA+PB ngắn nhất. Tính S= a+b
A. S=-1
B. S =5
C. S=-5
D. S= 1