Cho đường tròn (O) có đường kính bằng 12cm; hai điểm A,B thuộc đường tròn sao cho sđ cung AmB=120°. Tính độ dài cung AmB.
Những câu hỏi liên quan
Cho đường tròn tâm O bén kính 12cm và điểm M nằm ngoài đường tròn sao cho OM=20cm.Vẽ tiếp tuyến MA với đường tròn (O) (A là tiếp điểm).Độ dài của đoạn MA bằng : A.16cm B.20cm C.256cm D.8cm
Cho tam giác ABC có AB = AC nội tiếp đường tròn tâm O, đường cao AH
của tam giác cắt đường tròn (O) tại D
a) Chứng minh rằng AD là đường kính của đường tròn tâm O
b) Tính góc ACD
c) Cho BC = 12cm, AC = 10cm. Tính AH và bán kính của đường tròn tâm O
a) Ta có: ΔABC cân tại A
mà AH là đường cao ứng với cạnh BC
nên AH là đường trung tuyến ứng với cạnh BC
Ta có: AB=AC
nên A nằm trên đường trung trực của BC\(\left(1\right)\)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC\(\left(2\right)\)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(3)
Từ (1), \(\left(2\right),\left(3\right)\) suy ra A,O,H thẳng hàng
\(\Leftrightarrow A,O,H,D\) thẳng hàng
hay AD là đường kính của \(\left(O\right)\)
Đúng 0
Bình luận (0)
Một hình tròn tâm O có đường kính AB bằng 12cm. Hỏi đoạn thẳng OA là bao nhiêu cm?
OA là bán kính =>OA=\(\dfrac{AB}{2}=\dfrac{12}{2}=6cm\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
9 tháng 12 2021 lúc 22:08
Trong đường tròn (O), dây cung MN và cách O một khoảng bằng 8cm, biết MN = 12cm. bán kính của đường tròn (O) bằng
A. 10cm B. 16cm C. 6cm D. 4cm
Cho hai đường tròn O và o' có cùng bán kính cắt nhau tại A và B. đoạn nối tâm OA cắt đường tròn (O) và (O')theo thứ tự ở C và D biết ab=24cm cd=12cm bán kính mỗi đường trong là? giúp mình với ạ mình cảm ơn nhiềuuu
Tự vẽ hình nha=0
Ta có:
\(AC=\sqrt{\left(\dfrac{1}{2}CD\right)^2+\left(\dfrac{1}{2}AB\right)^2}=\sqrt{6^2+12^2}=6\sqrt{5}\left(cm\right)\)
\(R=\dfrac{OO'}{2}+\dfrac{CD}{2}\)
Mặt khác tứ giác `AOBO'` là hình thoi:
\(2R=OO'+CD=OO'+12\left(cm\right)\\ \Rightarrow R=10\left(cm\right)\)
`HaNa♫D`
Đúng 4
Bình luận (0)
Hai đường tròn tâm O và O' có cùng bán kính, cắt nhau ở A và B. Đoạn nối tâm OO' cắt các đường tròn (O), (O') lần lượt ở C và D. Biết AB = 24cm; CD = 12cm. Bán kính mỗi đường tròn là cm.
H la giao diem cua AB va CD ta co AH = BH =1/2 AB =12cm
cH=DH=6cm
=> AC=AD =\(\sqrt{12^2+6^2}\)=\(6\sqrt{5}\)......................
Đúng 0
Bình luận (0)
Hai đường tròn tâm O và O\' có cùng bán kính, cắt nhau ở A và B. Đoạn nối tâm OO\' cắt các đường tròn (O), (O\') lần lượt ở C và D. Biết AB = 24cm; CD = 12cm. Bán kính mỗi đường tròn là cm.
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh M A ⏜ và M B ⏜ có độ dài bằng nhau.
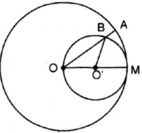
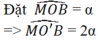(góc nội tiếp và góc ở tâ của đường tròn (O'))
Độ dài cung M A ⏜ là:
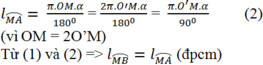
Đúng 0
Bình luận (0)
Cho đường tròn (O), bán kính OM. Vẽ đường tròn tâm O', đường kính OM. Một bán kính OA của đường tròn (O) cắt đường tròn (O') ở B.
Chứng minh cung Ma và cung MB có độ dài bằng nhau
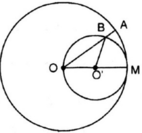
Kiến thức áp dụng
+ Trên đường tròn đường kính R, độ dài cung n0 bằng :
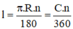
Đúng 0
Bình luận (0)