Bài 1: Cho tam giác ABC cân tại A,vẽ AH vuông góc với BC tại H. Biết AB10cm, BH6cma)Tính AHb)CM: Tam giác ABHtam giác ACHc)Trên BA lấy D, CA lấy E sao cho BDCE.CM tam giác HDE când)CM:AH là trung trực của DEBài 2: Cho tam giác ABC cân tại A.Kẻ BD vuông góc với AC,CE vuông góc với AB. BD cắt CE cắt nhau tại Ha)Tam giác ADBtam giác ACEb)Tam giác AHC cânc)ED song song BCd)AH cắt BC tại K, trên HK lất M sao cho K là trung điểm của HM.CM tam giác ACM vuôngBài 3:...
Đọc tiếp
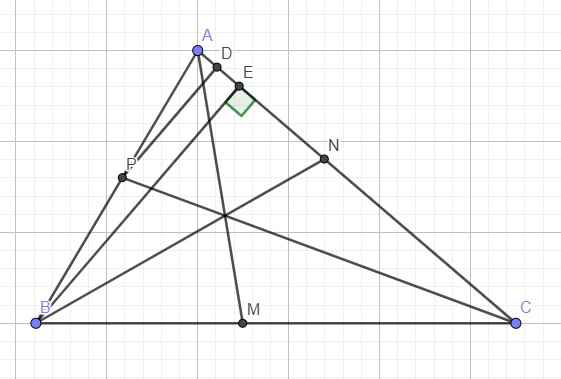
Bài 1: Cho tam giác ABC cân tại A,vẽ AH vuông góc với BC tại H. Biết AB=10cm, BH=6cm
a)Tính AH
b)CM: Tam giác ABH=tam giác ACH
c)Trên BA lấy D, CA lấy E sao cho BD=CE.CM tam giác HDE cân
d)CM:AH là trung trực của DE
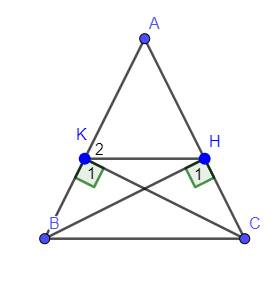
Bài 2: Cho tam giác ABC cân tại A.Kẻ BD vuông góc với AC,CE vuông góc với AB. BD cắt CE cắt nhau tại H
a)Tam giác ADB=tam giác ACE
b)Tam giác AHC cân
c)ED song song BC
d)AH cắt BC tại K, trên HK lất M sao cho K là trung điểm của HM.CM tam giác ACM vuông
Bài 3:Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ DE vuông góc với BC(E thuộc BC.Gọi F là giao điểm của BA và ED.CMR:
a)tam giác ABD=tam giác EBD
b)Tam giác ABE là tam giác cân
c)DF=DC
Bài 4: Cho tam giác ABC có góc A=90 độ,AB=8cm,AC=6cm
a) Tính BC
b)Trên cạnh AC lấy điểm E sao cho AE=2cm,trên tia đối của tia AB lấy D sao cho AD=AB.CM: tam giác BEC=tam giác DEC
c)CM: DE đi qua trung điểm cạnh BC