ĐK để căn có nghĩa:
`-4x^2+4x-2>=0`
`<=>2x^2-2x+1<=0`(vô lý)
Vì `2x^2-2x+1=2(x-1/2)^2+1/2>0`
`=>` không có gtrij của x thỏa đề bài.

giải giùm mình đi, thanks

giải giùm mình đi nha, thanks

1) 14x - 56 = 0

 ⇔14x = 56

 ⇔x = 4

2) 4 - 2x = 0

 ⇔2x = 4

 ⇔x = 2

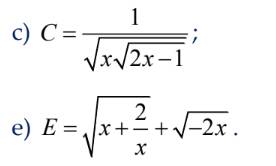
c

Để biểu thức C có nghĩa thì 

\(\sqrt{x\sqrt{2x-1}}>0\)

<=> \(\left\{{}\begin{matrix}x>0\\2x-1>0\Leftrightarrow x>\dfrac{1}{2}\end{matrix}\right.\Rightarrow x>\dfrac{1}{2}\)

Vậy để biểu thức C có nghĩa thì \(x>\dfrac{1}{2}\)

Giải câu e:

Điều kiện để biểu thức E có nghĩa:

\(\left\{{}\begin{matrix}x+\dfrac{2}{x}\ge0\\-2x\ge0\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}\dfrac{x^2+2}{x}\ge0\\x\le0\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}x>0\\x\le0\end{matrix}\right.\)

Vậy không tồn tại x để biểu thức E có nghĩa.

x nguyên,x khác -1

x nguyên,x khác 3

tik mik nha

để phân thức có giá trị thì x+1 khác 0

suy ra x khác -1 mà x nguyên

nên......

cái kia làm tương tự nha

tik mik nha

a: Để \(\dfrac{3}{x+1}\) là số nguyên thì \(3⋮x+1\)

\(\Leftrightarrow x+1\in\left\{1;-1;3;-3\right\}\)

hay \(x\in\left\{0;-1;2;-4\right\}\)

a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)

Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên

\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên

\(\Rightarrow11⋮4x-5\)

Vì \(x\in Z\) nên \(4x-5\in Z\)

\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)

\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)

Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).

b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)

Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)

       4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)

Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất

\(\Rightarrow4-x=1\Rightarrow x=3\)

\(\Rightarrow A=\dfrac{5}{4-3}=5\)

Vậy MaxA = 5 tại x = 3

c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).

Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)

Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất

\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất

Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\) 

       x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)

Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất

\(\Rightarrow x-3=-1\Rightarrow x=2\)

\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)

Vậy MaxB = -6 tại x = 2.

a) Để M nhận giá trị nguyên thì \(8x+1⋮4x-1\)

\(\Leftrightarrow8x-2+3⋮4x-1\)

mà \(8x-2⋮4x-1\)

nên \(3⋮4x-1\)

\(\Leftrightarrow4x-1\inƯ\left(3\right)\)

\(\Leftrightarrow4x-1\in\left\{1;-1;3;-3\right\}\)

\(\Leftrightarrow4x\in\left\{2;0;4;-2\right\}\)

\(\Leftrightarrow x\in\left\{\dfrac{1}{2};0;1;-\dfrac{1}{2}\right\}\)

mà x là số nguyên

nên \(x\in\left\{0;1\right\}\)

Vậy: \(x\in\left\{0;1\right\}\)

<=> x + 2 ≥ 0 và 3 - x ≥ 0 

<=> x ≥ -2 và x ≤ 3

vậy -2 ≤ x ≤ 3 

a.\(16-x^2=0\)

\(\Leftrightarrow x^2=16\)

\(\Leftrightarrow x^2=4^2\)

\(\Leftrightarrow x=\pm4\)

b.\(\left(x+1\right)^2+\left(2y-3\right)^{10}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\\left(2y-3\right)^{10}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2y-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\)

xác định khi:

(x + y)(6x – 6y) ≠ 0 ⇒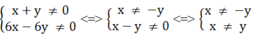 

Điều kiện x  ≠  ± y

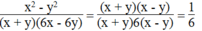
Vậy biểu thức không phụ thuộc vào x, y.

Biểu thức đâu bn ?????

Biểu thức là : A=(x+3)²+/y-2/

cái này em ko trả lời đc

xác định khi 4ax + 6x + 9y + 6ay ≠ 0

⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y)  ≠  0

Ta có: 2a + 3  ≠  0 ⇒ a  ≠  - 3/2 ; 2x + 3y  ≠  0 ⇒ x  ≠  - 3/2 y

Điều kiện: x  ≠  - 3/2 y và a  ≠  - 3/2

Vậy biểu thức không phụ thuộc vào x, y.