cho \(\Delta\)ABC = \(\Delta\) MNP với M = 40 độ ; 3B = 4C. tính số đo các góc của Δ ABC

Những câu hỏi liên quan
Cho ΔABC và ΔMNP; ∠A = ∠M =90o; AB = MN; BC = NP. C/M: ΔABC = ΔMNP ( giải theo 3 cách)
Các bạn giúp mình nhé!!!
Xét ΔABC vuông tại A và ΔMNP vuông tại M có
AB=MN
BC=NP
Do đo: ΔABC=ΔMNP
Đúng 0
Bình luận (0)
Cho ΔABC \(\backsim\) ΔMNP, khẳng định nào sau đây không đúng?
a) ΔMNP \(\backsim\) ΔABC
b) ΔBCA \(\backsim\) ΔNPM
c) ΔCAB \(\backsim\) ΔPNM
d) ΔACB \(\backsim\) ΔMNP
Khẳng định d) là khẳng định không đúng
=> ΔACB \(\backsim\) ΔMPN
Đúng 0
Bình luận (0)
Cho tứ diện SABC, lấy M, N, P lần lượt nằm trong các ΔSAB, ΔSBC, ΔSAC. Tìm giao tuyến của mp (MNP) với (ABC) và (SAB)
Cho \(\Delta ABC \backsim \Delta MNP\).
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).
a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\)và \(\Delta MNP\). Biết \(\widehat{A}\)= \(\widehat{M}\); \(\widehat{B}\)= \(\widehat{N}\)và chu vi \(\Delta ABC\)= chu vi \(\Delta MNP\). CMR: \(\Delta ABC=\Delta MNP\)
Cho biết \(\Delta ABC = \Delta MNP\), \(AC = 4\)cm, \(\widehat {MPN} = 45^\circ \). Tính độ dài cạnh MP và số đo góc ACB.
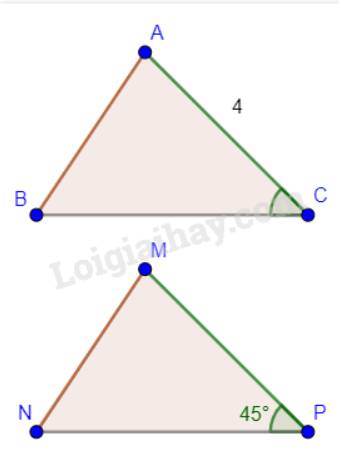
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).
Đúng 0
Bình luận (0)
1) Cho Delta ABCDelta DEF. Biết Delta ABC vuông tại A và B-C20. Tính số đo các góc của Delta DEF
2) Cho Delta ABCDelta MNP. Biết AB5cm, BC8cm, AC7cm, widehat{A}dfrac{4}{3}widehat{B}2widehat{C}. Tìm các cạnh và các góc của Delta MNP.
Mọi người giúp mình với
Đọc tiếp
1) Cho \(\Delta ABC=\Delta DEF\). Biết \(\Delta ABC\) vuông tại \(A\) và \(B-C=20\). Tính số đo các góc của \(\Delta DEF\)
2) Cho \(\Delta ABC=\Delta MNP\). Biết \(AB=5cm\), \(BC=8cm\), \(AC=7cm\), \(\widehat{A}=\dfrac{4}{3}\widehat{B}=2\widehat{C}\). Tìm các cạnh và các góc của \(\Delta MNP\).
Mọi người giúp mình với ![]()
Bài 1:
ΔABC=ΔDEF
nên \(\widehat{A}=\widehat{D}=90^0;\widehat{B}=\widehat{E};\widehat{C}=\widehat{F}\)
mà \(\widehat{B}-\widehat{C}=20^0\)
nên \(\widehat{E}-\widehat{F}=20^0\)
mà \(\widehat{E}+\widehat{F}=90^0\)
nên \(\widehat{E}=\dfrac{1}{2}\left(20^0+90^0\right)=55^0\)
=>\(\widehat{F}=35^0\)
Đúng 0
Bình luận (0)
Hai \(\Delta\)\(ABC\) và \(\Delta MNP\) có \(MP = AC, ABC = MNP = 90^o\). Điều kiện để \(\Delta ABC = \Delta MNP\) là:
A. BA = NP
B. \(\widehat{BAC} = \widehat{NMP}\)
C. BC = MN
D. Cả A, B, C
Xem thêm câu trả lời
Cho \(\Delta ABC=\Delta MNP\) biết góc B=60 độ, góc P=30 độ
a) CMR: \(\Delta ABC,\Delta MNP\) là các tam giác vuông
b) Vẽ MK vuông NP. Tính số đo góc NMK và góc PMK
Mk đag cần gấp, có ai giải giúp mk hk
Vì \(\Delta ABC=\Delta MNP\) nên:
N = B = 60o (2 góc tương ứng)
C = P = 30o (2 góc tương ứng)
Nên A = M = 180o - (60o + 30o) = 90o
Vậy \(\Delta ABC,\Delta MNP\) là các tam giác vuông (có góc bằng 90o)
Đúng 0
Bình luận (0)





















