Chứng minh từ A( 1; -1) kẻ được 2 tiếp tuyến vuông góc tới đồ thị hàm số \(y=x+\dfrac{1}{x+1}\)

Những câu hỏi liên quan
Cho A là tổng lập phương các số tự nhiên từ 1 đến n và B là bình phương tổng các số tự nhiên từ 1 đến n. Người ta đã chứng minh được rằng A=B. Bạn hãy chứng minh điều đó.
Bài 1: Cho ABC cân tại A, trung tuyến AM (M∈ BC).
a) Chứng minh ∆𝐴𝐵𝑀 = ∆𝐴𝐶𝑀
b) Từ M kẻ ME ⊥ AB, MF⊥AC (E𝜖𝐴𝐵, 𝐹𝜖𝐴𝐶). Chứng minh ∆𝐴𝐸𝐹 cân.
c) Chứng minh AM ⊥ EF
d) Trên tia đối của tia MF lấy điểm I sao cho IM = FM. Chứng minh EI //AM
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM Vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
=>ΔAFE cân tại A
c: AE=AF
ME=MF
=>AM là trung trực của FE
d: Xét ΔEFI có
EM là trung tuyến
EM=FI/2
=>ΔEFI vuông tại E
=>EF vuông góc FI
=>FI//AM
Đúng 0
Bình luận (0)
Từ 1 điểm A nằm ngoài đường tròn tâm ( O) kể các tiếp tuyến AM,AN với đường tròn chứng minh N là các tiếp tuyến điểm a) Chứng minh: 4 điểm A,M,O,N cùng nằm trên một đường tròn b) Chứng minh: AO vuông góc MN
a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=180^0\)
Do đó: OMAN là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Cho Δ ABC có AB=AC, M là trung điểm BC
1,Chứng minh Δ AMB = Δ AMC Từ M kẻ ME ⊥ AB (E ∈ AB)
2,MF ⊥ AC (M ∈ AC) Chứng minh AE =AF
3,Chứng minh EF//BC Từ B kẻ đường thẳng ⊥ AB, từ C kẻ đường thẳng ⊥ AC
4, hai đường thẳng này cắt nhau tại N. Chứng minh A,M,N thẳng hàng
a, xét tam giác AMB và tam giác AMC có :
AB=AC (gt)
MB=MC (gt)
AM là cạnh chung
suy ra: tam giác AMB = tam giác AMC (c.c.c)
b,Vì tam giác AMB = tam giác AMC ( câu a)
suy ra : góc B =góc C ( 2 góc tương ứng )
xét tam giác MBE và tam giác MCF có:
M1=M2 ( đối đỉnh )
B =C
MB=MC ( gt)
suy ra :tam giác MBE = tam giác MCF (g.c.g)
vì tam giác MBE = tam giác MCF (chứng minh trên)
ME=MF (2 cạch tương ứng )
xét tam giác AEM và tam giác AFM có :
E1=F1
AM là cạnh chung
ME=MF
suy ra : tam giác AEM = tam giác AFM (c.g.c)
vì tam giác AEM = tam giác AFM ( chứng minh trên)
suy ra :AE=AF
c, gọi điểm cắt nhau của EF và AM
Vì tam giác AMB = tam giác AMC (câu b)
suy ra : góc A1 = góc A2 ( 2 góc tương ứng ); góc M1 = góc M2 ( 2 góc tương ứng)
xét tam giác AEH và tam giác AFH có :
A1=A2
AE=AF
AH là điểm chung
suy ra : tam giác AEH = tam giác AFH (c.g.c)
suy ra góc H1= góc H2 ( 2 góc tương ứng)
mà H1+H2=180 (2 góc kề bù)
suy ra : H1=H2=90
suy ra AM vuông góc với EF
mà M1+M2=180
suy ra M1=M2=90
suy ra AM vuông góc với BC
mà AM vuông góc với EF
suy ra EF song song với BC ( 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau )
d, Ta có : AMB = NMC ( đối đỉnh )
+) AMB+AMC= 180 ( 2 góc kề bù )
mà AMC=NMC
suy ra AMB+NMC =180 (3)
mà AMB+NMC = AMN (4)
Từ (3),(4) suy ra : 3 điểm A,M,N thẳng hàng
Đúng 0
Bình luận (0)
1, xét tam giác AMB và tam giác AMC có:
AB=AC (gt)
MB=MC (gt)
Đúng 0
Bình luận (0)
Câu 1:Cho ∆ABC cân tại A,gọi M là trung điểm của BC sao cho BMMCa, Chứng minh rằng: ∆ABM∆ACMb, Chứng minh rằng:AM ⊥BCc, Từ M,vẽ MK⊥AC tại K,MH⊥AB tại H. Chứng minh rằng:BHCKd, Từ B,vẽ BP⊥AC tại P,tia MH và BP cắt nhau tại I.Chứng minh rằng: ∆IBM là ∆câne, Chứng minh rằng : BP//MK
Đọc tiếp
Câu 1:Cho ∆ABC cân tại A,gọi M là trung điểm của BC sao cho BM=MC
a, Chứng minh rằng: ∆ABM=∆ACM
b, Chứng minh rằng:AM ⊥BC
c, Từ M,vẽ MK⊥AC tại K,MH⊥AB tại H. Chứng minh rằng:BH=CK
d, Từ B,vẽ BP⊥AC tại P,tia MH và BP cắt nhau tại I.Chứng minh rằng: ∆IBM là ∆cân
e, Chứng minh rằng : BP//MK
a) Xét ΔABM và ΔACM có:
AB=AC ( ΔABC cân tại A)
Cạnh AM chung
MB=MC (gt)
⇒ ΔABM=ΔACM (c.c.c)
Vậy ΔABM=ΔACM
b) Vì ΔABM=ΔACM (cmt)
⇒ ∠AMB=∠AMC (2 góc tương ứng)
Ta có:∠AMB+∠AMC=180 ( 2 góc kề bù)
⇒ AMB=AMC=1800/2=900
⇒ AM⊥BC
Vậy AM⊥BC
c) Vì MK⊥AC (gt)
⇒ ∠MKA=∠MKC=900
Vì MH⊥AB (gt)
⇒ ∠MHA=∠MHB=900
Xét ΔHBM và ΔKCM có:
∠MHB∠=MKC=900
MB=MC (gt)
∠HMB∠=KMC (đối đỉnh)
⇒ ΔHBM = ΔKCM (cạnh huyền - góc nhọn)
⇒ BH=CK (2 cạnh tương ứng)
Vậy BH=CK
Mik mỏi tay lám rùi bạn tự làm phần sau nhé
Đúng 0
Bình luận (0)
xét ΔABM và ΔACM có:
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACM}\)(ΔABC cân tại A)
BM=CM(M là trung điểm của BC)
⇒ΔABM=ΔACM(c-g-c)
⇒\(\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)(1)
Mà \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)(2)
từ (1)và(2)⇒\(\widehat{ABM}=\widehat{ACM}=\dfrac{180^o}{2}=90^o\)
hay AM⊥BC(đ.p.ch/m)
xét 2 tam giác vuông HBM và KCM có
MC=MB(M là trung điểm của BC)
\(\widehat{HBM}=\widehat{KCM}\)(ΔABC cân tại A)
⇒ΔHBM=ΔKCM(c.huyền.g.nhọn)
⇒BH=CK(2 cạnh tương ứng)
vì BP⊥AC và MK⊥AC⇒BP//MK
vì ΔHBM=ΔKCM nên
⇒\(\widehat{HMB}=\widehat{KMC}\)(2 góc tương ứng)
Mà \(\widehat{KMC}=\widehat{PBM}\)(2 góc đồng vị)
⇒ΔIBM là tam giác cân(đ.p.ch/m)
vì BP⊥AC và MK⊥AC⇒BP//MK(đ.p.ch/m)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra:
A
F
.
A
B
A
E
.
A
C
b) Chứng minh
∠
A
E
F
∠
A
B
C
c) Cho
A
E
3
c
m
,...
Đọc tiếp
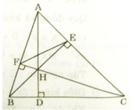
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh ΔAEB và ΔAFC đồng dạng. Từ đó suy ra: A F . A B = A E . A C
b) Chứng minh ∠ A E F = ∠ A B C
c) Cho A E = 3 c m , A B = 6 c m . Chứng minh rằng S A B C = 4 S A E F
d) Chứng minh A F F B . B D D C . C E E A = 1
a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
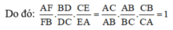
Đúng 4
Bình luận (0)
Bài 1. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH.
a) Chứng minh và .
b) Chứng minh
c) Trên tia HC, lấy HD = HA. Từ D vẽ đường thẳng song song AH cắt AC tại E. Chứng minh AE = AB.
Cho hình bình hành ABCD, E là điểm bất kì trên cạnh AB ( E≠A, E≠B ). Tia DE cắt AC ở F, cắt CB ở G.
a) Chứng minh ∆AEF ∆CDF; ∆AFD ∆CFG.
b) Chứng minh FD2 = FE.FG.
c) Từ F kẻ đường thẳng song song với đường thẳng AB cắt AD tại điểm H. Chứng minh 1:AE+1:AB=1:HF
Bài 1: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại D. Từ D kẻ DE vuông góc với BC . Đường thẳng ED cắt BA tại F. a/. Chứng minh▲BDA▲BDE. Từ đó suy ra ? b/. Chứng minh BD là đường trung trực của AE c/. Chứng minh BD vuông góc với CF.
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A. Đường phân giác của góc B cắt AC tại D. Từ D kẻ DE vuông góc với BC ![]() . Đường thẳng ED cắt BA tại F.
. Đường thẳng ED cắt BA tại F.
a/. Chứng minh▲BDA=▲BDE. Từ đó suy ra ![]() ?
?
b/. Chứng minh BD là đường trung trực của AE
c/. Chứng minh BD vuông góc với CF.
a) Xét ΔBDA vuông tại A và ΔBDE vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác)
Do đó: ΔBDA=ΔBDE(cạnh huyền-góc nhọn)
b) Ta có: ΔBDA=ΔBDE(cmt)
nên BA=BE(hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
Đúng 0
Bình luận (0)
Từ một điểm A nằm ngoài ( O;R) vẽ hai tiếp tuyến AB và AC
a) chứng minh ABOC nội tiếp
b) vẽ cát tuyến ADE, chứng minh: AD.AE=AB.AB
c) Gọi I là trung điểm DE, chứng minh : A;O;I;C nằm trên 1 đường tròn
d) chứng minh IA là phân giác của góc BIC























