Cho a, b là các số thực thuộc khoảng ( 0 ; π / 2 ) và thỏa mãn điều kiện cota-tan( π / 2 -b)=a-b. Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Cho a, b là các số thực thuộc khoảng 0 ; π 2 thỏa mãn điều kiện cota - tan π 2 - b = a-b. Tính giá trị biểu thức P = 3 a + 7 b a + b
A. P = 5
B. P = 2
C. P = 4
D. P = 6
Cho a, b là các số thực thuộc khoảng 0 ; π 2 và thỏa mãn điều kiện c o t a - tan π 2 - b = a - b .Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Cho a,b,c là các số thực thuộc khoảng (0:1) thỏa mãn abc=(1-a)(1-b)(1-c)
Tìm GTNN của P=a+b+c\(+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Cho 2 số thực a,b thuộc khoảng (0; 1) thỏa mãn
(a3 + b3)(a + b) - ab(a - 1)(b - 1) = 0. Giá trị lớn nhất của
P = xy là
\(\left(a^3+b^3\right)\left(a+b\right)=ab\left(1-a\right)\left(1-b\right)\)
\(\Leftrightarrow\left(1-a\right)\left(1-b\right)=\left(\dfrac{a^2}{b}+\dfrac{b^2}{a}\right)\left(a+b\right)\ge\left(a+b\right)^2\ge4ab\)
\(\Rightarrow1+ab-4ab\ge a+b\ge2\sqrt{ab}\)
\(\Rightarrow3ab+2\sqrt{ab}-1\le0\)
\(\Leftrightarrow\left(\sqrt{ab}+1\right)\left(3\sqrt{ab}-1\right)\le0\)
\(\Leftrightarrow ab\le\dfrac{1}{9}\)
Biết S=(a;b) là tất cả các giá trị thực của m để phương trình
cos
3
x
-
cos
2
x
+
m
cos
x
-
1
=
0
có đúng 8 nghiệm thực phân biệt thuộc khoảng 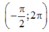 . Tính tổng T=a+b
. Tính tổng T=a+b
A. 4
B. -2
C. 17 4
D. 25 4
Đáp án D
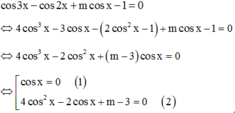
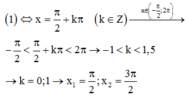
→
(1) có 2 nghiệm thuộc 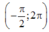
Để phương trình có đúng 8 nghiệm thuộc khoảng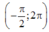 thì (2) phải có đúng 6 nghiệm phân biệt thuộc
thì (2) phải có đúng 6 nghiệm phân biệt thuộc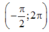 và khác
x
1
;
x
2
và khác
x
1
;
x
2
Đặt t = cos x ( - 1 ≤ x ≤ 1 ) , (2) trở thành f ( t ) = 4 t 2 - 2 t + m - 3 = 0 ( 3 )
+ Nếu
0
<
t
<
1
thì phương trình cosx=t có 3 nghiệm phân biệt thuộc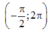
+ Nếu
-
1
<
t
<
0
thì phương trình cosx=t có 2 nghiệm phân biệt thuộc khoảng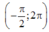
Do đó (2) có đúng 6 nghiệm phân biệt thuộc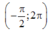
⇔ (3) có 2 nghiệm t 1 ; t 2 thỏa mãn 0 < t 1 < t 2 < 1
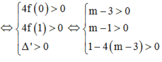

Biết rằng T=[a;b] là tập tất cả các giá trị thực của tham số m để phương trình log 1 3 2 x + log 3 2 + 1 - 1 - 5 m = 0 có ít nhất một nghiệm thuộc khoảng 1 ; 3 2 2 . Tính a 2 + b 2
A. a 2 + b 2 = 4
B. a 2 + b 2 = 6
C. a 2 + b 2 = 8
D. a 2 + b 2 = 10
Đáp án A
Đặt t = log 3 2 x + 1 ⇒ t ' = log 3 x log 3 2 x + 1 . 1 x ln 3 ≥ 0 ∀ x ∈ 1 ; 3 2 2
Suy ra t ∈ 1 ; 3 : P T : t 2 + t - 2 - 5 m = 0 ⇔ t 2 + t - 2 = 5 m
Xét f t = t 2 + t - 2 , t ∈ 1 ; 3 ⇒ f ' t = 2 t + 1 > 0 nên hàm số đồng biến trên [1;3]
Do đó để phương trình có nghiệm thì 5 m ∈ f 1 ; f 3 ⇒ m ∈ 0 ; 2
Biết S= (a;b) là tập tất cả các giá trị thực của m để phương trình cos3x - cos2x+ mcosx-1 = 0 có đúng 8 nghiệm thực phân biệt thuộc khoảng - π 2 ; 2 π .Tính tổng T = a+b.
A. 4..
B. -2
C. 17 4
D. 25 4
Cho 3 số thực a,b,c thỏa mãn a= -2b - 5c. CMR PT \(ax^2+bx+c=0\) có ít nhất 1 no thuộc khoảng (0;1)
\(a=-2b-5c\Rightarrow a+2b=-5c\)
- Với \(c=0\Rightarrow a=-2b\Rightarrow-\dfrac{b}{a}=\dfrac{1}{2}\)
\(ax^2+bx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{b}{a}=\dfrac{1}{2}\in\left(0;1\right)\end{matrix}\right.\) (thỏa mãn)
- Với \(c\ne0\)
Hàm \(f\left(x\right)=ax^2+bx+c\) liên tục trên R
\(f\left(0\right)=c\) ;
\(f\left(\dfrac{1}{2}\right)=\dfrac{a}{4}+\dfrac{b}{2}+c=\dfrac{a+2b+4c}{4}=\dfrac{-5c+4c}{4}=-\dfrac{c}{4}\)
\(\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)=-\dfrac{c^2}{4}< 0;\forall c\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) do \(\left(0;\dfrac{1}{2}\right)\subset\left(0;1\right)\)
cho nửa khoảng A=(-\(\infty\);-m] và khoảng B=(2m-5;23). gọi S là tập hợp các số thực m để \(A\cup B=A\). hỏi S là tập con của tập hợp nào sau đây?
A. (-\(\infty\);-23)
B. (-\(\infty\);0]
C. (-23;+\(\infty\))
D. \(\varnothing\).
Để A hợp B=A thì B là tập con của A
=>2m-5<23 và 23<=-m
=>2m<28 và -m>=23
=>m<=-23 và m<14
=>m<=-23
=>Chọn B