Các câu hỏi tương tự
Cho hai số thực a, b thỏa mãn điều kiện
3
a
−
4
b
0
và biểu thức
P
log
a
a
3
4
b
+
3
16
log
3...
Đọc tiếp
Cho hai số thực a, b thỏa mãn điều kiện 3 a − 4 > b > 0 và biểu thức P = log a a 3 4 b + 3 16 log 3 a 4 + b a 2 có giá trị nhỏ nhất. Tính tổng S=3a+b
A. S = 8
B. S = 13 2
C. S = 25 2
D. S = 14
Cho các số dương a, b, c thỏa mãn
a
+
b
+
c
π
. Gía trị lớn nhất của biểu thức
P
c
o
s
b
+
c
o
s
c
-
4
s
i
n
3
a
2
là A.
4
6
B.
2...
Đọc tiếp
Cho các số dương a, b, c thỏa mãn a + b + c = π . Gía trị lớn nhất của biểu thức P = c o s b + c o s c - 4 s i n 3 a 2 là
A. 4 6
B. 2 3 6
C. 4 3 6
D. 1 6
Cho các số dương a, b, c thỏa mãn
a
+
b
+
c
π
. Gía trị lớn nhất của biểu thức
P
c
o
s
b
+
c
o
s
c
-
4
s
i
n
3
a
2
là A.
4
6
B.
2...
Đọc tiếp
Cho các số dương a, b, c thỏa mãn a + b + c = π . Gía trị lớn nhất của biểu thức P = c o s b + c o s c - 4 s i n 3 a 2 là
A. 4 6
B. 2 3 6
C. 4 3 6
D. 1 6
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
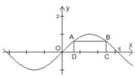
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho các số thực a, b đồng thời thỏa mãn
3
-
a
2
b
1152
và
log
5
(
a
+
b
)
...
Đọc tiếp
Cho các số thực a, b đồng thời thỏa mãn 3 - a 2 b = 1152 và log 5 ( a + b ) = 2 . Tính giá trị biểu thức P = a - b.
Cho hai số thực a, b thỏa mãn đồng thời các đẳng thức
3
-
2
.
2
b
1152
và
log
5
a
+
b
2
. Tính giá trị biểu thức
P
a
-
b
A. -3 B. -9 C. 8 D. -6
Đọc tiếp
Cho hai số thực a, b thỏa mãn đồng thời các đẳng thức 3 - 2 . 2 b = 1152 và log 5 a + b = 2 . Tính giá trị biểu thức P = a - b
A. -3
B. -9
C. 8
D. -6
Cho các số thực a và b thỏa mãn:
(
2
+
a
)
(
1
+
b
)
9
2
Giá trị nhỏ nhất của biểu thức:
P
16
+
a
4
+
4
1
+
b
4
nằm trong khoảng A. (8,1;8,3) B. (4;4,2) C. (8,3...
Đọc tiếp
Cho các số thực a và b thỏa mãn: ( 2 + a ) ( 1 + b ) = 9 2 Giá trị nhỏ nhất của biểu thức: P = 16 + a 4 + 4 1 + b 4 nằm trong khoảng
A. (8,1;8,3)
B. (4;4,2)
C. (8,3;8,5)
D. (12,4;12,6)
Cho hai số thực a,b thỏa mãn điều kiện
a
2
+
b
2
1
và
log
a
2
+
b
2
a
+
b
≥
1
. Giá trị lớn nhất của biểu thức P 2a + 4b – 3 là A. ...
Đọc tiếp
Cho hai số thực a,b thỏa mãn điều kiện a 2 + b 2 > 1 và log a 2 + b 2 a + b ≥ 1 . Giá trị lớn nhất của biểu thức P = 2a + 4b – 3 là
A. 2 10
B. 10
C. 10 2
D. 1 10
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện
3
a
5
b
15
-
c
. Tìm giá trị nhỏ nhất của biểu thức
P
a
2
+
b
2
+
c
2
-
4
a
+...
Đọc tiếp
Gọi a, b, c là ba số thực khác 0 thay đổi và thỏa mãn điều kiện 3 a = 5 b = 15 - c . Tìm giá trị nhỏ nhất của biểu thức P = a 2 + b 2 + c 2 - 4 a + b + c
A. - 3 - log 5 3
B. -4
C. - 2 - 3
D. - 2 - log 5 3




