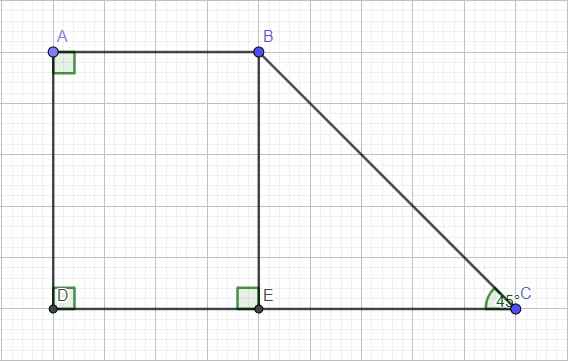
cho hình thang vuông ABCD có ^A=^D=90o ; ^C=30o ,AD=2√2cm , CD = 3√6cm.Tính diện tích tam giác ABC

Những câu hỏi liên quan
Cho hình thang vuông ABCD (góc A = góc D = 90o ) có AC vuông góc với BD tại H .Biết HB=8cm, HD=18cm .Tính diện tích hình thang
Ta có: \(AH^2=HD.HB=18.8=144\Rightarrow AH=12\) (cm)
\(\Rightarrow AD=\sqrt{AH^2+HD^2}=\sqrt{12^2+18^2}=6\sqrt{13}\)
\(AB=\sqrt{12^2+8^2}=4\sqrt{13}\)
Ta có: \(DH^2=HA.HC\Rightarrow CH=\dfrac{DH^2}{HA}=\dfrac{18^2}{12}=27\)
\(\Rightarrow CD=\sqrt{CH^2+HD^2}=\sqrt{27^2+18^2}=9\sqrt{13}\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).AD=\dfrac{1}{2}\left(4\sqrt{13}+9\sqrt{13}\right).6\sqrt{13}\)
\(=507\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD (A = D = 90o) có AB = 1/2 CD. Gọi H là hình chiếu của D lên AC. Gọi M là trung điểm của HC. C/m BMD=90o
Gọi K là trung điểm của HD
Xet ΔHDC có HK/HD=HM/HC
nên KM//DC
=>KM vuông góc với AD
Xét ΔADM có
MK,DH là các đường cao
MK cắt DH tại K
Do đó: K làtrực tâm
=>AK vuông góc với DM
Xét tứ giác ABMK có
AB//MK
AB=MK
Do đó; ABMK là hình bình hành
=>AK//BM
=>BM vuông góc với DM
Đúng 1
Bình luận (0)
Gọi K là trung điểm của HD
Xet ΔHDC có HK/HD=HM/HC
nên KM//DC
=>KM vuông góc với AD
Xét ΔADM có
MK,DH là các đường cao
MK cắt DH tại K
Do đó: K làtrực tâm
=>AK vuông góc với DM
Xét tứ giác ABMK có
AB//MK
AB=MK
Do đó; ABMK là hình bình hành
=>AK//BM
=>BM vuông góc với DM
Đúng 0
Bình luận (0)
Bài 8: cho hình thang vuông ABCD có góc A = góc D = 90o . AB = AD = 2cm, DC = 4cm. Tính hai góc còn lại của hình thang
Cho hình thang vuông ABCD có
A
^
D
^
90
o
,
AB
AD
2
cm
,
CD
2
AB
.
Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB A.
40
π
3...
Đọc tiếp
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB = AD = 2 cm , CD = 2 AB . Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB
A. 40 π 3 cm 3
B. 16 π 3 cm 3
C. 8 πcm 3
D. 8 π 3 cm 3
Đáp án A
Ta có thể tích khối tròn xoay tạo thành bằng hiệu thể tích hình trụ bán kính đáy AD, chiều cao CD trừ cho thể tích nón đỉnh B, bán kính đáy BM chiều cao CM.
Ta có
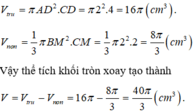
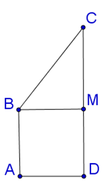
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có
A
^
D
^
90
o
, ABAD2cm, CD2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
Đọc tiếp
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB=AD=2cm, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
![]()
![]()
![]()
![]()
Chọn B
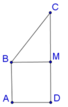
Ta có thể tích khối tròn xoay tạo thành bằng hiệu
thể tích hình trụ bán kính đáy AD, chiều cao
CD trừ cho thể tích nón đỉnh B, bán kính đáy
BM chiều cao CM.
Ta có:

Đúng 0
Bình luận (0)
Hình thang vuông ABCD có A = D = 90o , đường chéo BD vuông góc BC và BD = BC
a) Tính các góc trong hình thang
b) Biết AB = 3cm. Tính BC và CD
Lời giải:
a. $BD\perp BC, BD=BC$ nên tam giác $BDC$ vuông cân tại $B$
$\Rightarrow \widehat{C}=45^0$
$\widehat{ABC}=180^0-\widehat{C}=180^0-45^0=135^0$
b.
Ta có: $\widehat{ABD}=\widehat{ABC}-\widehat{DBC}=135^0-90^0=45^0$ nên tam giác $ABD$ vuông cân tại $A$
$\Rightarrow AD=AB=3$
Áp dụng định lý Pitago:
$BD=\sqrt{AB^2+AD^2}=\sqr{3^2+3^2}=3\sqrt{2}$ (cm)
$BC=BD=3\sqrt{2}$ (cm)
Tam giác $BDC$ vuông cân tại $B$ nên áp dụng định lý Pitago:
$DC=\sqrt{BC^2+BD^2}=\sqrt{(3\sqrt{2})^2+(3\sqrt{2})^2}=6$ (cm)
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD,góc A và góc D bằng 90o. Đường chéo BD vuông góc với BC, biết AD=12cm, DC=25cm. Tính các cạnh còn lại.
Tính diện tích hình thang vuông ABCD ( góc A = góc D = 90o ), biết góc C = 45o, AB = 2cm, CD = 4cm.
Cho hình thang \(ABCD\) có \(\widehat{A}\)=\(\widehat{D}\)=90o, \(\widehat{C}\)= 45o. Biết đường cao của hình thang bằng 4cm, \(AB+CD=10cm\). Tính 2 đáy.
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thang vuông ABCD có góc A=góc B=90o và AD=2BC. kẻ AH vuông góc với BD. Gọi I là trung điểm của HD. cmr CI vuông góc với AI