Tìm tiệm cận ngang của đồ thị các hàm số sau:
a) \(y=f\left(x\right)=\dfrac{x-1}{4x+1};\) b) \(y=g\left(x\right)=\dfrac{\sqrt{x}}{\sqrt{x}+2}\).
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\) có đường tiệm cận ngang đi qua điểm M (-2;1)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = 1
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1
tìm tham số thỏa mãn yêu cầu bài toán:
a) tìm m biết đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\) có đường tiệm cận ngang đi qua điểm A (-1;3)
b) biết rằng đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\) có đường tiệm cận ngang là đường thẳng y = -2
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2
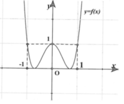
Cho hàm số
y
=
f
(
x
)
=
a
x
4
+
b
x
2
+
c
có đồ thị như hình bên dưới. Tìm tổng tất cả các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
=
x
(
x
-
1
)
f
(
x
)
-
1
![]()
![]()
![]()
![]()
Gọi S là tập hợp các giá trị nguyên của m sao cho đồ thị hàm số y = \(\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}\) có bốn đường tiệm cận (bao gồm tiệm cận đứng và tiệm cận ngang). Tính số phần tử của tập S
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\lim\limits_{x\rightarrow+\infty}\dfrac{2019}{\sqrt{17-\dfrac{1}{x^2}}-m}=\dfrac{2019}{\sqrt{17}-m}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\dfrac{2019}{m-\sqrt{17}}\)
Với \(m\ne\sqrt{17}\Rightarrow\) đồ thị hàm số luôn có 2 tiệm cận ngang
Với \(m=\sqrt{17}\) đồ thị hàm số ko có tiệm cận ngang
Xét phương trình: \(\sqrt{17x^2-1}=m\left|x\right|\)
- Với \(m< 0\Rightarrow\) pt vô nghiệm \(\Rightarrow\) ko có tiệm cận đứng \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
- Với \(m\ge0\)
\(\Leftrightarrow17x^2-1=m^2x^2\Leftrightarrow\left(17-m^2\right)x^2=1\)
+ Nếu \(\left[{}\begin{matrix}m\ge\sqrt{17}\\m\le-\sqrt{17}\end{matrix}\right.\) pt vô nghiệm \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
+ Nếu \(-\sqrt{17}< m< \sqrt{17}\) pt có 2 nghiệm \(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy \(m=\left\{0;1;2;3;4\right\}\) có 5 phần tử
cho hàm số \(y=f\left(x\right)\) liên tục trên R thỏa
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\) , \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\dfrac{1}{2}\)
tìm số đường tiệm cận củ đồ thị hàm số đã cho
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\)
Hàm số có 1 tiệm cận ngang là \(y=-\dfrac{1}{2}\)
83. Biết rằng hs f(x)= ax^3 + bx^2 +cx =d đạt cực đại tại điểm x =3 ,đạt cực tiểu tại điểm x =-2 . Tổng số đg tiệm cận đứng và tiệm cận ngang của đồ thị hs y = \(\dfrac{\left(x-1\right)\left(\sqrt{x+2}\right)}{\sqrt{f\left(x\right)-f\left(1\right)}}\) là?
Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → x 0 f x = y 0 h o ặ c lim x → x 0 f x = y 0
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → - ∞ f x = y 0 h o ặ c lim x → + ∞ f x = y 0
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = + ∞ h o ặ c lim x → x 0 - f x = - ∞
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = - ∞ h o ặ c lim x → x 0 - f x = - ∞
Trong các mệnh đề trên, số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
Chọn C
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.
26. Tìm số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số y = \(\dfrac{\sqrt{x-1}}{x^2-3x+2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
Nêu cách tìm ra tiệm cận ngang và tiệm cận dứng của đồ thị hàm số. Áp dụng để tìm các tiệm cận của đồ thị hàm số: Áp dụng để tìm các tiệm cận của đồ thị hàm số y = 2 x + 3 2 - x
- Cách tìm tiệm cận ngang:
+ Tính các giới hạn 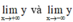
+ Nếu 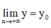 hoặc
hoặc 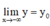 thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
- Cách tìm tiệm cận đứng:
Đường thẳng x = x o là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
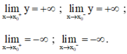
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \(\dfrac{x+\sqrt{x^2+1}}{x+1}\)
Lời giải:
TXĐ: \((-\infty; -1)\cup (-1;+\infty)\)
\(\lim\limits_{x\to +\infty}y=\lim\limits_{x\to +\infty}\frac{1+\sqrt{1+\frac{1}{x}}}{1+\frac{1}{x}}=\frac{1+1}{1}=2\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to -\infty}\frac{-1+\sqrt{1+\frac{1}{x^2}}}{-1+\frac{1}{-x}}=\frac{-1+1}{-1}=0\)
Do đó ĐTHS có 2 TCN là $y=0$ và $y=2$
\(\lim\limits_{x\to -1-}y=\lim\limits_{x\to -1-}\frac{x+\sqrt{x^2+1}}{x+1}=-\infty\) do \(\lim\limits_{x\to -1-}(x+\sqrt{x^2+1})=\sqrt{2}-1>0\) và \(\lim\limits_{x\to -1-}\frac{1}{x+1}=-\infty\)
Tương tự \(\lim\limits_{x\to -1+}y=+\infty\) nên $x=-1$ là TCĐ của đths
Vậy có tổng 3 TCN và TCĐ