a: Xét ΔABC có \(AC^2=AB^2+BC^2\)

nên ΔABC vuông tại B

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=HB\cdot HC\)

\(\Leftrightarrow AH^2=18\cdot32=576\)

hay AH=24cm

Ta có: BH+CH=BC

nên BC=18+32=50cm

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=32\cdot50=1600\\AC^2=18\cdot50=900\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=40cm\\AC=30cm\end{matrix}\right.\)

a) áp dụng đ/l pitago zô tam giác zuông abh ta đc

=> AB^2=AH^2+HB^2

=> AH^2=Ab^2-HB^2

=> AH=24

áp dụng dl pitago zô tam giác zuông ahc

=> AC^2=AH^2+HC^2

=> AC=40

b) Tco : CH+HB=32+18=50

Tam giac ABC có

\(\hept{\begin{cases}AB^2+AC^2=40^2+30^2=2500\\BC^2=50^2=2500\end{cases}}\)

=> \(AB^2+AC^2=BC^2\)

=> tam giác abc zuông

https://olm.vn/hoi-dap/tim-kiem?id=1153717&subject=1&q=++++++++++cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+t%E1%BA%A1i+A+.K%E1%BA%BB+AH+vu%C3%B4ng+g%C3%B3c+BC+t%E1%BA%A1i+H.Bi%E1%BA%BFt+BH=18cm,HC=32cm.T%C3%ADnh+AC+++++++++

Ta có: BC = HB+HC = 9+16=25cm

Áp dụng định lý pitago vào tam giác vuông ABC, có:

\(BC^2=AB^2+AC^2\)

\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=\sqrt{225}=15cm\)

Áp dụng định lý pitago vào tam giác vuông ABH, có:

\(AB^2=AH^2+BH^2\)

\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=\sqrt{144}=12cm\)

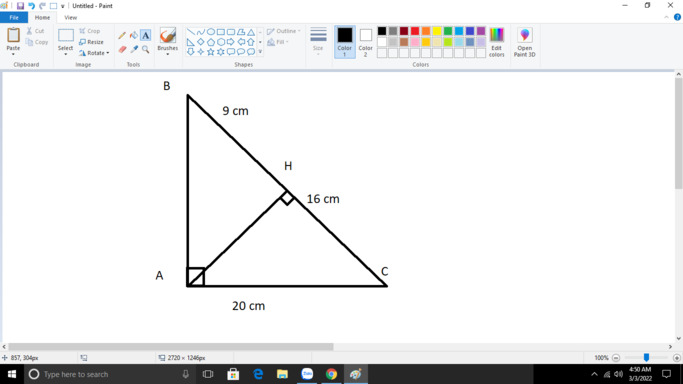
\(BC=BH+HC\)

\(\Rightarrow BC=9cm+16cm=25\left(cm\right)\)

\(\text{Xét }\Delta ABC\text{ vuông tại }A\text{ có:}\)

\(BC^2=AB^2+AC^2\)

\(\Rightarrow AB^2=BC^2-AC^2\text{(định lí Py ta go đảo)}\)

\(\Rightarrow AB^2=25^2-20^2=625-400=225\left(cm\right)\)

\(\Rightarrow AB=\sqrt{225}=15\left(cm\right)\)

\(\text{Xét }\Delta AHC\text{ vuông tại }H\text{ có:}\)

\(AC^2=AH^2+HC^2\)

\(\Rightarrow AH^2-AC^2-HC^2\text{(định lí Py ta go đảo)}\)

\(\Rightarrow AH^2=20^2-16^2=400-256=144\left(cm\right)\)

\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)

Ap dụng định lý Pytago ta có:

        \(BC^2=AB^2+AC^2\)

\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)

\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)

Ta có hình vẽ: 

 Áp dụng định lý Pitago. Ta có:

BC² = AB² + AC² <=> 6² + 8² = 100 cm²

100 = 10 x 10

=> BC = 10 cm

 Áp dụng công thức Heron để tính chiều cao. Ta có:

  \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)  (p là chu vi, S là diện tích, a,b,c là độ dài 3 cạnh)

  Ta có: Chu vi tam giác là: 6 + 8 + 10 =24 cm

Vậy \(S=\sqrt{24\left(24-6\right)\left(24-8\right)\left(24-10\right)}=48\sqrt{42}\)

   Để tính chiều cao AH, ta lấy 2 lần diện tích chia cho đáy ( BC) sẽ có được chiều cao

2 lần diện tích là: \(48\sqrt{42}.2=96\sqrt{42}\)

\(\Rightarrow AH=96\sqrt{42}:10=\frac{24\sqrt{42}}{25}\)

 Độ dài cạnh BH là:  (Bạn tự làm)

Độ dài cạnh HC là: (Bạn tự làm nhé)

dfaishfdkasjnMajka  ưi

BC=25cm

\(AB=\sqrt{9\cdot25}=15\left(cm\right)\)

=>AC=20cm

AH=12

a) Xét tam giác BAH và tam giác CAH, có:

AH: cạnh chung

AB = AC ( tam giác ABC cân tại A )

góc AHB = góc AHC ( = 90 độ )

-> tam giác BAH = tam giác CAH ( ch-cgv )

-> HB = HC ( 2 cạnh tương ứng )

b) Xét tam giác FBH và tam giác ECH, có:

HB = HC ( cmt )

góc D = góc E ( = 90 độ )

góc B = góc C ( tam giác ABC cân tại A )

-> tam giác FBH = tam giác ECH ( ch-gn )

-> HF = HE ( 2 cạnh tương ứng )

-> tam giác HEF là tam giác cân tại H

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có

AB=AC(ΔABC cân tại A)

AH chung

Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)

Suy ra: BH=CH(hai cạnh tương ứng)

b) Xét ΔFHB vuông tại F và ΔEHC vuông tại E có

BH=CH(cmt)

\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)

Do đó: ΔFHB=ΔEHC(cạnh huyền-góc nhọn)

Suy ra: HF=HE(Hai cạnh tương ứng)

Xét ΔHEF có HF=HE(cmt)

nên ΔHEF cân tại H(Định nghĩa tam giác cân)