cho hình vuông ABCD có M thuộc BC đường thẳng vuông góc AM tại M cắt CD tại E

Những câu hỏi liên quan
cho hình vuông ABCD có E thuộc BC ; đường thẳng (d) đi qua A và vuông góc vs AE cắt CD tại F. trung tuyến AM của tam giác AEF cắt CD tại K . biết A(-6;6) ;M( -4;2) ; K( -3;0) .Tìm điểm D
Cho hình vuông ABCD, lấy M thuộc BC. Đường thẳng AM cắt CD tại P. Kẻ đường thẳng EF bất kì vuông góc với AM( E thuộc AB, F thuộc CD). Đường phân giác của góc DAM cắt CD tại K. CMR:
a)EF=BM+DK
b)1/AM2+ 1/AP2 =1/AB2
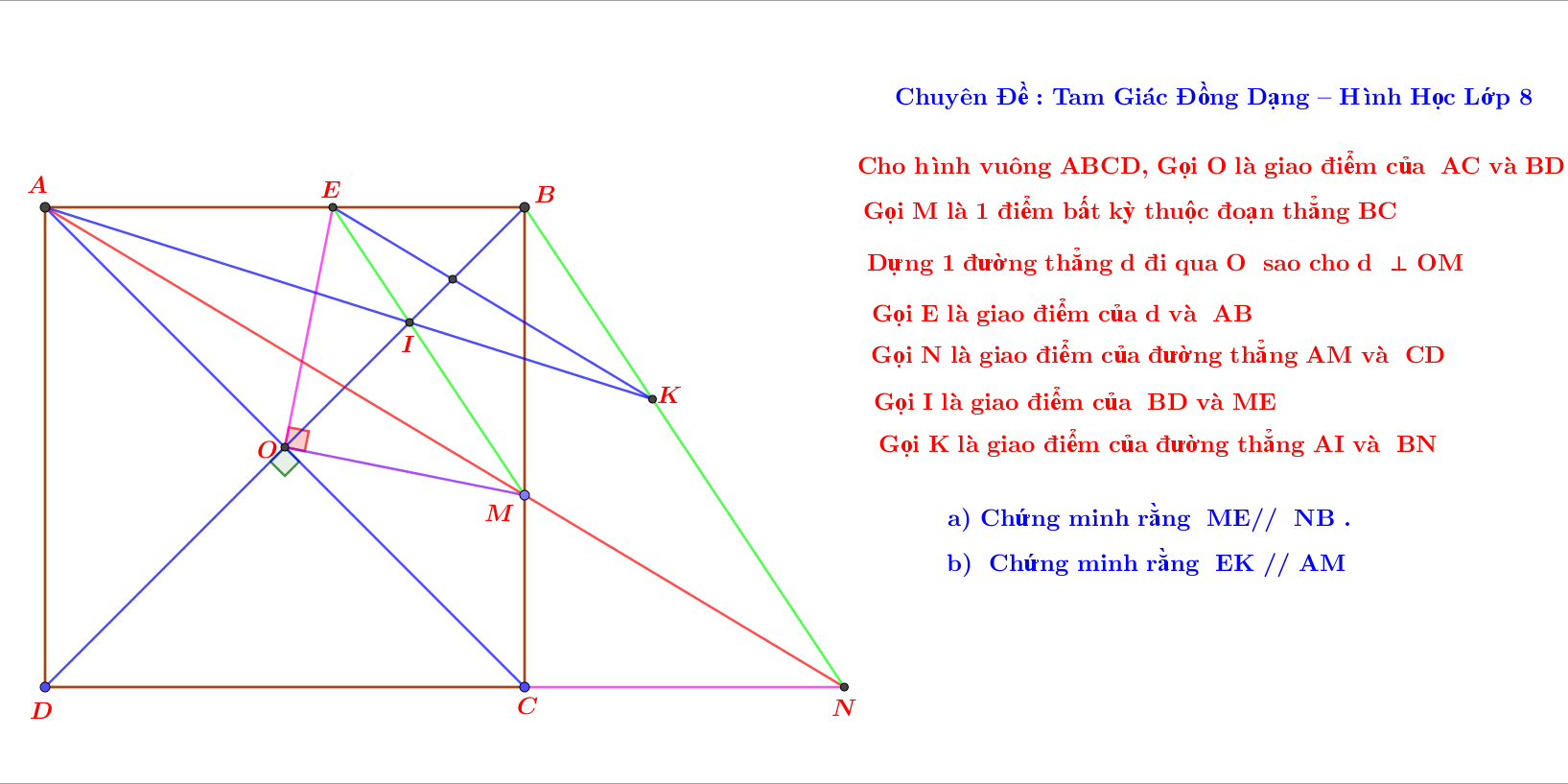
Cho hình vuông ABCD tâm O, điểm M thuộc cạnh BC. Qua O kẻ đường thẳng vuông góc với OM, cắt AB tại E, và AM cắt CD tại N.
a) Chứng minh rằng ME // NB .
b) Đường thẳng BD cắt EM tại I , và AI cắt NB tại K. Chứng minh rằng EK // AM .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
a. \(\widehat{AOE}=90^0-\widehat{BOE}=\widehat{BOM}\)
\(\Rightarrow\)△AOE=△BOM (g-c-g). \(\Rightarrow AE=BM;BE=CM\).
△MCN có: CN//AB \(\Rightarrow\dfrac{MN}{AM}=\dfrac{CM}{BM}=\dfrac{BE}{AE}\Rightarrow\)ME//NB.
Đúng 2
Bình luận (0)
Cho hình vuông ABCD. Lấy điểm M trên cạng BC. Đường thẳng AM cắt đường thẳng CD tại P. Đường thẳng EF vuông góc với AM và trong đó E, F tương ứng nằm trên AB và CD. Đường phân giác góc DAM cắt CD tại K. Chứng minh rằng: EF = BM + DK
Trong mặt phẳng hệ tọa độ Oxy, cho hình vuông ABCD và điểm E thuộc cạnh BC. Một đường thẳng qua A vuông góc với AE cắt CD tại F. Đường thẳng chứa đường trung tuyến AM của tam giác AEF cắt CD tại K. Tìm tọa độ điểm D biết A(-6;6). M(-4;2) và K(-3;0)
Có 2 tam giác vuông \(\Delta ABE=\Delta ADF\) vì \(AB=AD\) và \(\widehat{BAE}=\widehat{DAF}\) cùng phụ với \(\widehat{DAE}\)
Suy ra tam giác AEF vuông cân và \(ME=MA=MF\Rightarrow AM\perp EF\)
Ta có \(\overrightarrow{MA}=\left(2;-4\right)\), đường thẳng EF đi qua M có phương trình :
\(2\left(x+4\right)-4\left(y-2\right)=0\Leftrightarrow x-2y+8=0\)
Bây giờ tìm tọa độ các điểm E, F thỏa mãn ME=MA=MF. Gọi T(x;y) thuộc đường thẳng EF, thì x=2t-8; y=t, \(t\in R\)
Khi đó \(MT=MA\Leftrightarrow\left(2t-8+4\right)^2+\left(1-2\right)^2=2^2+\left(-4\right)^2=20\)
\(\Leftrightarrow5\left(t-2\right)^2=20\Leftrightarrow t\left(t-4\right)=0\Leftrightarrow\)\(\begin{cases}t=0\\t=4\end{cases}\)
Như vậy có 2 điểm \(t_1\left(-8;0\right);t_2\left(0;4\right)\) ( Chính là 2 điểm E và F) thuộc đường thẳng EF mà \(MT_1=MA\)
- Trường hợp \(E\left(-8;0\right);F\left(0;4\right)\). Do F thuộc đường thẳng CD nên đường thẳng CD nhận \(\overrightarrow{KF}=\left(3;4\right)\) làm vec tơ chỉ phương.
Phương trình đường thẳng CD là \(\begin{cases}x=3t\\y=4+4t\end{cases}\) (\(t\in R\)).
Khi đó \(D\left(3t;4+4t\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{KF}.\overrightarrow{AD}=0\Rightarrow3\left(3t+6\right)+4\left(-2+4t\right)=0\Leftrightarrow t=-\frac{2}{5}\Rightarrow D\left(-\frac{6}{5};\frac{12}{5}\right)\)
- Trường hợp \(F\left(-8;0\right);E\left(0;4\right)\), đường thẳng CD nhận \(\overrightarrow{FK}=\left(5;0\right)\) làm vec tơ chỉ phương
Phương trình CD : \(\begin{cases}x=-8+5t\\y=0\end{cases}\) \(\left(t\in R\right)\)
Khi đó \(D\left(-8+5t;0\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{FK}.\overrightarrow{AD}=0\Leftrightarrow5\left(-2+5t\right)=0\Leftrightarrow t=\frac{2}{5}\Rightarrow D\left(-6;0\right)\)
Đúng 0
Bình luận (0)
cho hình vuông abcd vẻ một tia a cắt BC,CD tại M,N đường thẳng A vuông góc AM cắt BC CD tại IQ chứng minh rằng tam giác AMI AMQ Cân Gọi E F là trung điểm của NI MQ chưng minh rằng EFDB thẳng hàng
Cho hình vuông ABCD,trên BC lấy điểm M ( M không thuộc B,C).Gọi E là giao điểm của AM với CD. Từ A kẻ đường thẳng vuông góc với AM, cắt DC tại F a,CMR: AF bình =FD.FE b,Tam giác AFM vuông cân tại A c,1/AF bình+1/AE bình không đổi khi M di chuyển trên BC d,Từ C kẻ CK vuông góc AF.Tính FAD
Cho hình vuông ABCD. Lấy điểm M trên cạng BC. Đường thẳng AM
cắt đường thẳng CD tại P. Đường thẳng EF vuông góc với AM và trong đó
E, F tương ứng nằm trên AB và CD. Đường phân giác góc DAM cắt CD tại
K. Chứng minh rằng:
a) EF = BM + DK
Cho hình thang vuông ABCD và điểm M thuộc cạnh BC. Kéo dài AM cắt tia CD tại N. Qua A kẻ đường thẳng vuông góc với AM cắt tia CB tại E.
a) Chứng minh: AE = AN
b) Chứng minh: 1/AB2 = 1/AM2 + 1/AN2