nhờ cả vào mn ạ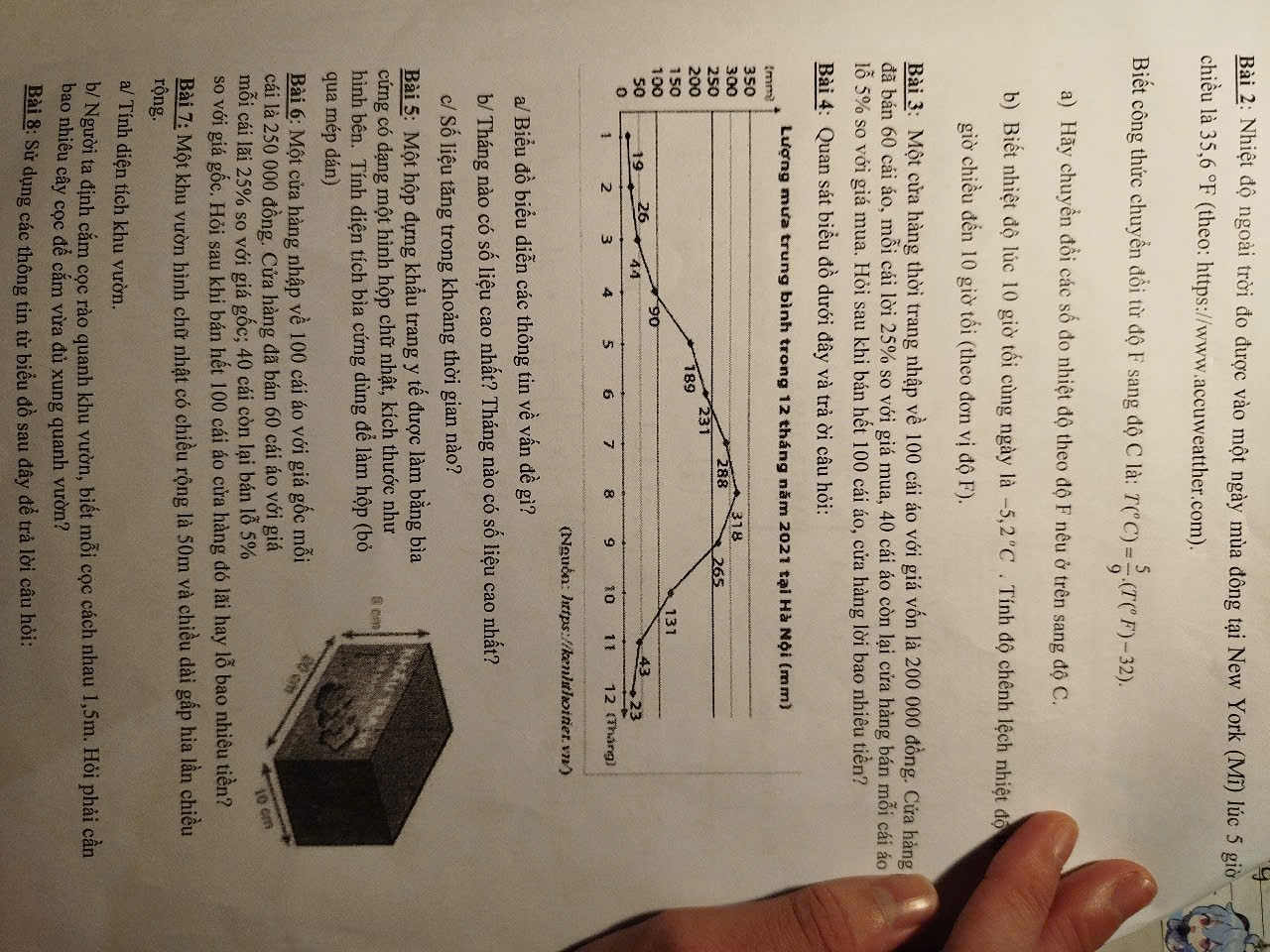


Những câu hỏi liên quan
Mình đang gấp lắm mn ơi, nhờ mn giúp mình câu 3 vs ạ, nếu đc cả câu 4 nữa thì mình cảm ơn mn nhiều.

Nhờ mn tìm giúp em mấy đề hình ôn thi vào 10 với ạ ! Cho em xin với ạ !
Tham khao
Bài 1: Cho nửa đường tròn (O) đường kính AB= 2R, dây cung AC. Gọi M là điểm chính giữa cung AC. Một đường thẳng kẻ từ điểm C song song với BM và cắt AM ở K , cắt OM ở D. OD cắt AC tại H.
1. Chứng minh CKMH là tứ giác nội tiếp.
2. CMR : CD = MB ; DM = CB.
3. Xác điểm C trên nửa đường tròn (O) để AD chính là tiếp tuyến của nửa đường tròn.
Bài 2: Cho ABC có 3 góc nhọn. Đường tròn có đường kính BC cắt hai cạnh AB, AC lần lượt tại các điểm E và F ; BF cắt EC tại H. Tia AH BC tại điểm N.
a) CMR: tứ giác HFCN là tứ giác nội tiếp.
b) CMR: FB là tia phân giác của góc EFN.
c) Nếu AH = BC. Hãy tìm số đo góc BAC trong ΔABC.

Bài 3: Cho nửa đường tròn tâm O và nó có đường kính AB. Từ một điểm M nằm trên tiếp tuyến Ax của nửa đường tròn, ta vẽ tiếp tuyến thứ hai tên gọi là MC (trong đó C là tiếp điểm). Từ C hạ CH vuông góc với AB, MB cắt (O) tại điểm Q và cắt CH tại điểm N. Gọi g I = MO ∩ AC. CMR:
a) Tứ giác AMQI là tứ giác nội tiếp.
b) Góc AQI = góc ACO
c) CN = NH.
(Trích đề thi tuyển sinh vào lớp 10 năm học 2009-2010 của sở GD&ĐT Tỉnh Bắc Ninh)

Bài 4: Cho đường tròn (O) có đường kính là AB. Trên AB lấy một điểm D nằm ngoài đoạn thẳng AB và kẻ DC là tiếp tuyến của đường tròn (O) (với C là tiếp điểm). Gọi E là hình chiếu hạ từ A xuống đường thẳng CD và F là hình chiếu hạ từ D xuống AC.
Chứng minh:
a) Tứ giác EFDA là tứ giác nội tiếp.
b) AF là tia phân giác của góc EAD.
c) Tam giác EFA và BDC là hai tam giác đồng dạng.
d) Hai tam giác ACD và ABF có cùng diện tích với nhau.
(Trích đề thi tốt nghiệp và xét tuyển vào lớp 10- năm học 2000- 2001)

Bài 5: Cho tam giác ABC (BAC < 45o) là tam giác nội tiếp trong nửa đường tròn tâm O có đường kính AB. Vẽ tiếp tuyến của đường tròn (O) tại C và gọi H là hình chiếu kẻ từ A đến tiếp tuyến . Đường thẳng AH cắt đường tròn (O) tại M (M ≠ A). Đường thẳng kẻ từ M vuông góc với AC cắt AC tại K và AB tại P.
a) CMR tứ giác MKCH là một tứ giác nội tiếp.
b) CMR: MAP là tam giác cân.
c) Hãy chỉ ra điều kiện của ΔABC để M, K, O cùng nằm trên một đường thẳng.

Đúng 3
Bình luận (1)
Viết chương trình nhập dữ liệu là ma trận đối xứng vào mảng hai chiều. Nhờ mn giúp mik vs ạ cảm ơn mn rất nhiều 😆😆
uses crt;
var a:array[1..100,1..100]of integer;
i,n,m,j:integer;
begin
clrscr;
readln(n,m);
for i:=1 to n do
for j:=1 to m do
readln(a[i,j]);
readln;
end.
Đúng 1
Bình luận (0)
Cả nhà ai biết làm câu 3 chỉ em với ạ,em cảm ơn😊 kết quả trong sách viết là S={0} nha,ai chỉ em nhớ xem kết quả đúng ko nhờ mn ạ
`3)(x+4)/(x-3)-(x-3)/(x+4)=(x^2+18x+7)/(x^2+x-12)`
`đk:x ne 3,x ne -4`
Nhân 2 vế với `(x-3)(x+4) ne 0` ta có:
`(x+4)^2-(x-3)^2=x^2+18x+7`
`<=>x^2+8x+16-x^2+6x-9=x^2+18x+7`
`<=>14x+7=x^2+18x+7`
`<=>x^2+4x=0`
`<=>x(x+4)=0`
Vì `x ne -4=>x+4 ne 0`
`<=>x=0`
Vậy `S={0}`
Đúng 2
Bình luận (1)
Nhờ mn ạ
6 unhealthy
7 behavior
8 southest
9 industrial
10 belief
bài 2
1 silent
2 holes
3 of
4 will
5 take
Đúng 5
Bình luận (0)
6 unhealthy
7 behavior
8 southest
9 industrial
10 belief
bài 2
1 silent
2 holes
3 of
4 will
5 take
Đúng 1
Bình luận (0)
Nhờ mn ạ
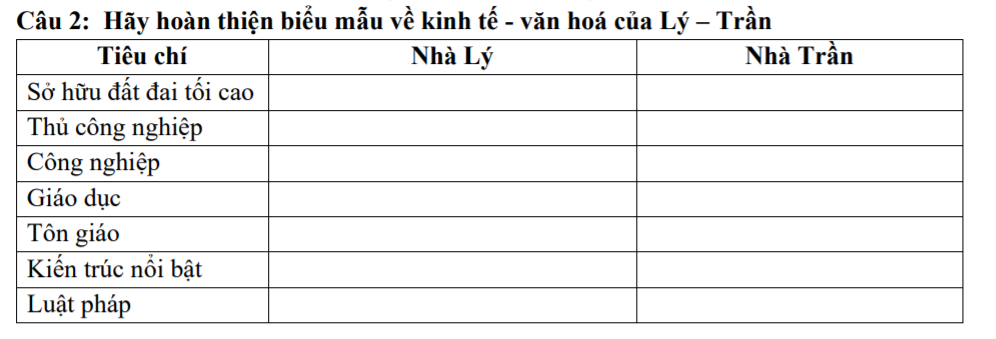 NHỜ MN Ạ!
NHỜ MN Ạ!
Nhờ mn giúp ạ
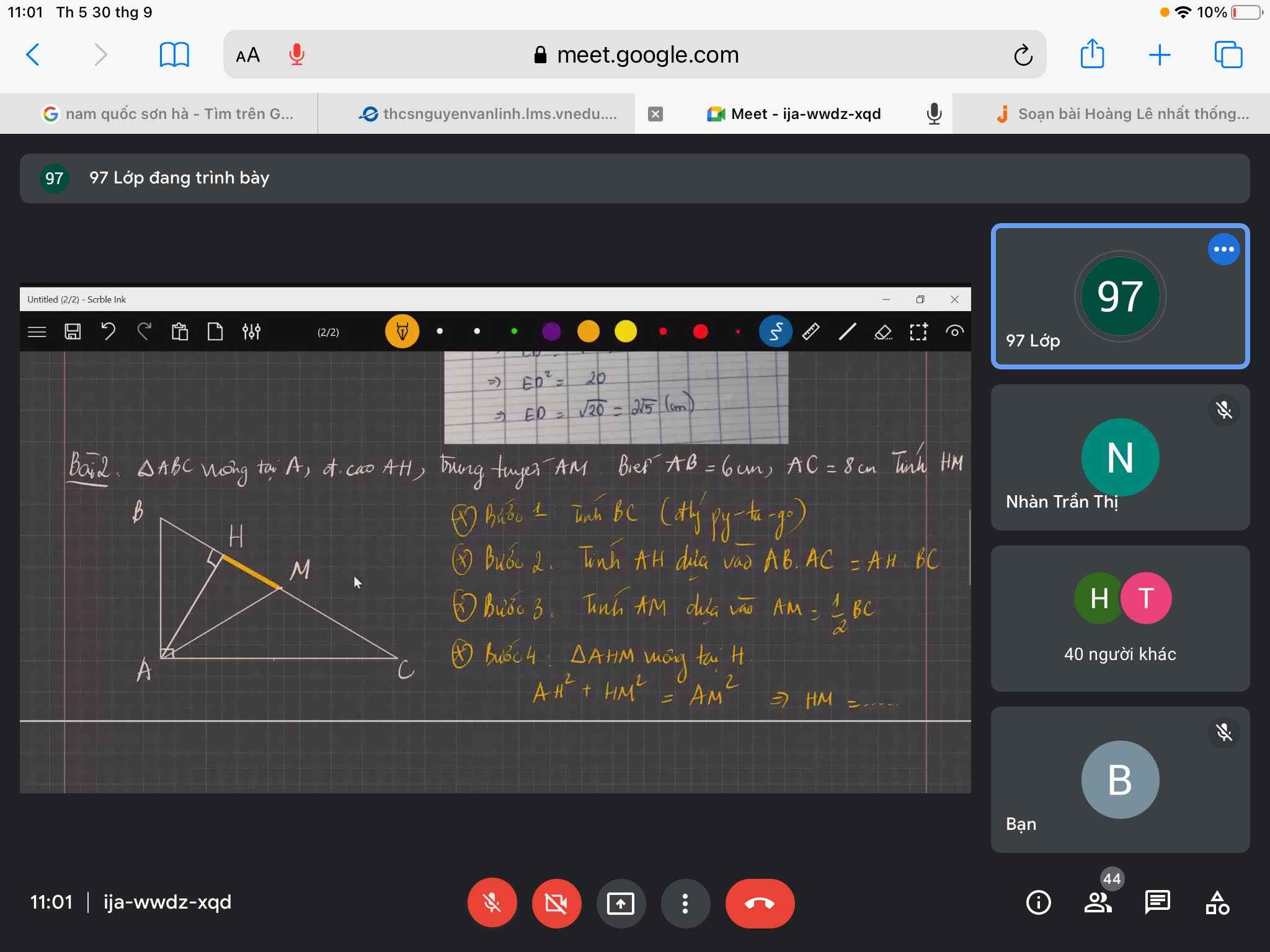
Nhờ mn giúp ạ
Áp dụng pytago: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Áp dụng HTL: \(AB\cdot AB=AH\cdot BC\Rightarrow AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=5\left(cm\right)\)
Áp dụng pytago: \(HM=\sqrt{AM^2-AH^2}=1,4\left(cm\right)\)
Đúng 1
Bình luận (0)
Nhờ mn giải giúp ạ. Cảm ơn mn rất nhiều🙆🏻♀️

































