Giải giúp e 2 câu này với ạ

Những câu hỏi liên quan
ai giải hộ e 2 câu này với ạ .nhanh giúp e với


giúp e giải 2 câu này với ạ! e cảm ơn
Ai giúp e bài này với ạ: Giải phương trình( giải giúp e câu 3 và câu 4 phần này với ạ)

Câu 3 và caau4 bài giải phương trình nhé
Đúng 0
Bình luận (0)
Bài 3. Đặt ẩn phụ là
\(a=2x-\frac{5}{x}\\\)
\(b=x-\frac{1}{x}\)
pt <=> \(b-a=\sqrt{a}-\sqrt{b}\\ \)
\(\left(\sqrt{b}-\sqrt{a}\right)\left(\sqrt{b}+\sqrt{a}\right)=-\left(\sqrt{b}-\sqrt{a}\right)\\ \)
\(\left(\sqrt{b}-\sqrt{a}\right)\left(\sqrt{b}+\sqrt{a}+1\right)=0\)
tới đây xét 2 TH bạn tự giải nhé
Đúng 0
Bình luận (0)
giúp e giải gấp 2 câu này với ạ e cảm ơn vì hiện tại e cần gấp
Giúp e giải câu này với ạ e cảm ơn
Giúp e giải câu này với ạ
Giải giúp e đạo hàm câu này với ạ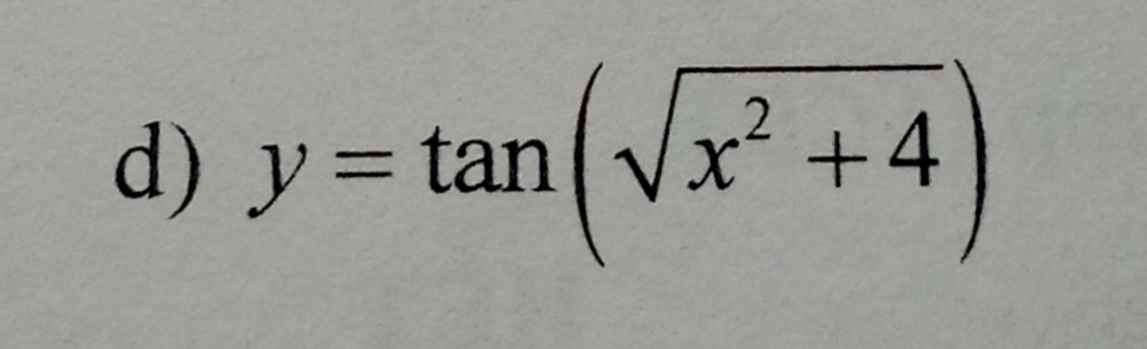
\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)
Đúng 0
Bình luận (0)
mn giúp e câu này với, giải chi tiết ra cho e ạ! 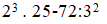
\(=8\cdot25-72:9=200-8=192\)
Đúng 4
Bình luận (0)
Giúp e giải 6 câu ôn tập này với ạ, e cần gấp
câu 6: bài học: hãy là chính mình, biết sống hết mình, làm tốt những trách nhiệm, bổn phận của bản thân sẽ được mọi người tôn trọng, yêu quý
Đúng 0
Bình luận (0)
mọi người giúp em với ạ, e cần giải thích của câu này ạ

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.
Đúng 0
Bình luận (0)























