Bài 4. (3,5 điểm) Cho đường tròn (O;R) đường kính AB. Điểm C thuộc đường tròn
sao cho AC > CB; C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông
góc với AC tại I.
a) Chứng minh 4 điểm C, H, O, I cùng thuộc một đường tròn

Những câu hỏi liên quan
Bài 4. (3,5 điểm) Cho điểm M nằm ngoài đường tròn (0;R) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn (0) (A, B là các tiếp điểm). Kẻ đường kính AC của đường tròn (0). Gọi H là giao điểm của AB và OM. 1) Chứng minh bốn điểm A, O, B, M cùng thuộc một đường tròn. 2) Tính tỷ số OH/OM. 3) Gọi E là giao điểm của CM và đường tròn (0). Chứng minh HE vuông góc BE.
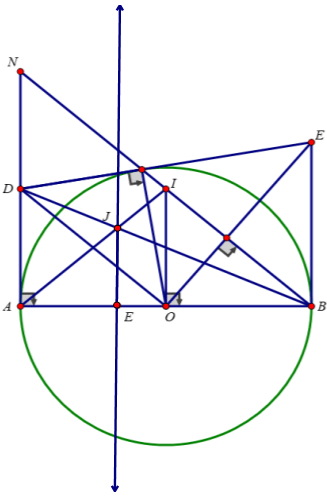
Bài IV (3,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. Điểm C thuộc đoạn AB (C khác B;A). Trên cùng nửa mặt phẳng bờ AB có chứa nửa (O;R). Vẽ nửa đường tròn tâm I, đường kính AC và nửa đường tròn tâm J, đường kính BC. Qua C kẻ đường thẳng vuông góc với AB cắt (O;R) tại D. DA cắt nửa đường tròn tâm I tại M, DB cắt nửa đường tròn tâm J tại N 1) Chứng minh rằng: Tứ giác MDNC là hình chữ nhật2) Chứng minh rằng: Tứ giác AMNB nội tiếp.3) Chứng minh rằng: OD vuông góc MN4) Tì...
Đọc tiếp
Bài IV (3,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. Điểm C thuộc đoạn AB (C khác B;A). Trên cùng nửa mặt phẳng bờ AB có chứa nửa (O;R). Vẽ nửa đường tròn tâm I, đường kính AC và nửa đường tròn tâm J, đường kính BC. Qua C kẻ đường thẳng vuông góc với AB cắt (O;R) tại D. DA cắt nửa đường tròn tâm I tại M, DB cắt nửa đường tròn tâm J tại N
1) Chứng minh rằng: Tứ giác MDNC là hình chữ nhật
2) Chứng minh rằng: Tứ giác AMNB nội tiếp.
3) Chứng minh rằng: OD vuông góc MN
4) Tìm vị trí của C trên AB để bán kính đường tròn ngoại tiếp tứ giác AMNB lớn nhất.
Bài III (3,5 điểm) Cho (OR; ), đường thẳng d không đi qua O cắt đường tròn ( )O tại C và D. Lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M . Qua M vẽ tiếp tuyến MAMB, với đường tròn (A, B là tiếp điểm), OM cắt AB tại E. Gọi H là trung điểm củaCD. Chứng minh rằng1) Bốn điểm AOBM, , , cùng nằm trên một đường tròn (I). Điểm H có thuộc đường tròn (I) nói trên không? Vì sao?
Đọc tiếp
Bài III (3,5 điểm) Cho (OR; ), đường thẳng d không đi qua O cắt đường tròn ( )O tại C và D. Lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M . Qua M vẽ tiếp tuyến MAMB, với đường tròn (A, B là tiếp điểm), OM cắt AB tại E. Gọi H là trung điểm củaCD. Chứng minh rằng
1) Bốn điểm AOBM, , , cùng nằm trên một đường tròn (I). Điểm H có thuộc đường tròn (I) nói trên không? Vì sao?
Bài III (3,5 điểm) Cho (OR; ), đường thẳng d không đi qua O cắt đường tròn ( )O tại C và D. Lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M . Qua M vẽ tiếp tuyến MAMB, với đường tròn (A, B là tiếp điểm), OM cắt AB tại E. Gọi H là trung điểm củaCD. Chứng minh rằng1) Bốn điểm AOBM, , , cùng nằm trên một đường tròn (I). Điểm H có thuộc đường tròn (I) nói trên không? Vì sao?2) AB vuông góc với OM .3) Tích OEOM. không đổi khi M thay đổi.4) Khi M di chuyển trên đường th...
Đọc tiếp
Bài III (3,5 điểm) Cho (OR; ), đường thẳng d không đi qua O cắt đường tròn ( )O tại C và D. Lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M . Qua M vẽ tiếp tuyến MAMB, với đường tròn (A, B là tiếp điểm), OM cắt AB tại E. Gọi H là trung điểm củaCD. Chứng minh rằng
1) Bốn điểm AOBM, , , cùng nằm trên một đường tròn (I). Điểm H có thuộc đường tròn (I) nói trên không? Vì sao?
2) AB vuông góc với OM .
3) Tích OEOM. không đổi khi M thay đổi.
4) Khi M di chuyển trên đường thẳng d thì đường thẳng AB luôn đi qua một điểm cố định.
Bài 5 (3,5 điểm)Cho đường tròn (O) đường kính BC = 2R và dây cung AB = R
a) Chứng minh AABC vuông tại A. Tính độ dài cạnh AC theo R.
b) Trên tia OA lấy điểm D sao cho A là trung điểm của OD. Chứng minh DB là tiếp tuyển của đường tròn (O).
c) Vẽ tiếp tuyến DM với đường tròn (O) (M là tiếp điểm). Chứng minh ABDM là tam giác đều.
d) Chứng minh tứ giác AMOB là hình thoi.
Câu 4 (3,5 điểm) Cho nửa đường tròn tâm O, đường kính BC, 4 là điểm chính giữa cung BC. Dung hình bình hành ABCD. Gọi H là chân đường cao kẻ từ 4 xuống BD, E là giao điểm của BD với nửa đường tròn (O). a. Chứng minh tứ giác AHCD nội tiếp. b. Chứng minh 4OE = 2CAH c. Chứng minh DE.DB = 2.4C2
Bài 3: (3,5 điểm) Cho đường tròn (O), đường kính AB bằng 2R. Qua A và B lần lượtkẻ 2 tiếp tuyền d và d với đường tròn. Từ một điểm M trên đường thẳng d vẽ tia MOcắt đường thẳng d ở P. Từ O vẽ một tia vuông với MP và cắt đường thắng d ở Da) Chứng minh O là trung điểm của MP và tam giác MDP cânb) Hạ OI 1 MD (I E MD). Chứng minh IE (O) và DM là tiếp tuyến của đườngtròn (0).c) Chứng minh : Tích AM.BD không phụ thuộc vào vị trí của điểm M.d) Tính diện tích của tứ giác AMDB theo R khi MO 2R
Đọc tiếp
Bài 3: (3,5 điểm) Cho đường tròn (O), đường kính AB bằng 2R. Qua A và B lần lượt
kẻ 2 tiếp tuyền d và d' với đường tròn. Từ một điểm M trên đường thẳng d vẽ tia MO
cắt đường thẳng d' ở P. Từ O vẽ một tia vuông với MP và cắt đường thắng d' ở D
a) Chứng minh O là trung điểm của MP và tam giác MDP cân
b) Hạ OI 1 MD (I E MD). Chứng minh IE (O) và DM là tiếp tuyến của đường
tròn (0).
c) Chứng minh : Tích AM.BD không phụ thuộc vào vị trí của điểm M.
d) Tính diện tích của tứ giác AMDB theo R khi MO = 2R
Bài 4: (3,5 điểm) Cho đường tròn (O ; R) đường kính AB và điểm M bất kì thuộc đường tròn (M ≠ A, B) . Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt AN ở D.a) Chứng minh: 4 điểm A, D, M , O cùng thuộc một đường trònb) Chứng minh: OD // BM và suy ra D là trung điểm của ANc) Đường thẳng kẻ qua O và vuông góc với BM cắt tia DM ở E. Chứng minh: BE là tiếp tuyến của đường tròn (O ; R)d) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM...
Đọc tiếp
Bài 4: (3,5 điểm) Cho đường tròn (O ; R) đường kính AB và điểm M bất kì thuộc đường tròn (M ≠ A, B) . Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt AN ở D.
a) Chứng minh: 4 điểm A, D, M , O cùng thuộc một đường tròn
b) Chứng minh: OD // BM và suy ra D là trung điểm của AN
c) Đường thẳng kẻ qua O và vuông góc với BM cắt tia DM ở E. Chứng minh: BE là tiếp tuyến của đường tròn (O ; R)
d) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM tại I. Gọi giao điểm của AI và BD là J. Khi điểm M di động trên (O ; R) thì J chạy trên đường nào?
\(\text{a) Xét tứ giác ADMO có:}\)
∠DMO =90o (do M là tiếp tuyến của (O))
∠DAO =90o (do AD là tiếp tuyến của (O))
=> ∠DMO + ∠DAO = 180o
=> Tứ giác ADMO là tứ giác nội tiếp.
\(\text{b) Do D là giao điểm của 2 tiếp tuyến DM và DA nên OD là tia phân giác của ∠AOM}\)
=>(AOD = \(\frac{1}{2}\)∠AOM
Mặt khác ta có (ABM là góc nội tiếp chắn cung AM
=> ∠ABM = \(\frac{1}{2}\)∠AOM
=> ∠AOD = ∠ABM
Mà 2 góc này ở vị trí đồng vị
=> OD // BM
Xét tam giác ABN có:
OM// BM; O là trung điểm của AB
=> D là trung điểm của AN
c) Ta có: ΔOBM cân tại O ;OE ⊥MB =>OE là đường trung trực của MB
=>EM = EB => ΔMEB cân tại E => ∠EMB = ∠MEB (1)
ΔOBM cân tại O => ∠OMB = ∠OBM (2)
Cộng (1) và (2) vế với vế, ta được:
∠EMB + ∠OMB = ∠MEB + ∠OBM ⇔ ∠EMO =∠EOB ⇔ ∠EOB =90o
=>OB ⊥ BE
Vậy BE là tiếp tuyến của (O).
d) Lấy điểm E trên tia OA sao cho OE = \(\frac{OA}{3}\)
Xét tam giác OAI có OI vừa là đường cao vừa là trung tuyến
=> Tam giác OAI cân tại I => IA = IB; ∠IBA = ∠IAB
Ta có:
\(\hept{\begin{cases}\widehat{IBA}=\widehat{IAB}\\\widehat{IBA}+\widehat{INA}=90^0\\\widehat{NAI}+\widehat{IAB}=\widehat{NAB}=90^0\end{cases}}\)
=> ∠NAI = ∠INA => ΔINA cân tại I => IA = IN
Tam giác NAB vuông tại A có: IA = IN = IB
=> IA là trung tuyến của tam giác NAB
Xét ΔBNA có:
IA và BD là trung tuyến; IA ∩ BD = {J}
=> J là trọng tâm của tam giác BNA
Xét tam giác AIO có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}=\frac{2}{3}\Rightarrow\text{JE}\text{//}OI\)
=> J nằm trên đường thẳng d vuông góc với AB và cách O một khoảng bằng R/3.
Phần đảo: Lấy điểm J' bất kì thuộc đường thẳng d
Do d// OI (cùng vuông góc AB) nên ta có:
\(\frac{\text{AJ}}{AI}=\frac{AE}{A0}\)
\(\text{MÀ}\frac{AE}{AO}=\frac{2}{3}\Rightarrow\frac{\text{AJ}}{AI}=\frac{2}{3}\)
AI là trung tuyến của tam giác NAB
=> J' là trọng tâm tam giác NAB
Vậy khi M di chuyển trên (O) thì J di chuyển trên đường thẳng d vuông góc với AB và cách O một khoảng là R/3.
HÌNH Ở TRONG THỐNG KÊ HỎI ĐÁP NHA
Bài 4 (3,5 điểm): 1. Cho tam giác abc có ba góc nhọn nội tiếp (O:R). Hạ các đường cao AD, BE của tam giác cắt nhau tại H và kẻ đường kính CF của (O) a) Chứng minh các điểm A, E, D, B cùng nằm trên một đường tròn. b) Chứng minh tứ giác AHBF là hình bình hành. c) Cho (O) và dây AB cố định, điểm C di chuyển trên cung lớn AB. Chứng minh rằng độ dài bán kính đường tròn ngoại tiếp tam giác CDE luôn không đổi.
Đọc tiếp
Bài 4 (3,5 điểm):
1. Cho tam giác abc có ba góc nhọn nội tiếp (O:R). Hạ các đường cao AD, BE của tam giác cắt nhau tại H và kẻ đường kính CF của (O)
a) Chứng minh các điểm A, E, D, B cùng nằm trên một đường tròn.
b) Chứng minh tứ giác AHBF là hình bình hành.
c) Cho (O) và dây AB cố định, điểm C di chuyển trên cung lớn AB. Chứng minh rằng độ dài bán kính đường tròn ngoại tiếp tam giác CDE luôn không đổi.
Bài 4: ( 3,5 điểm ) Cho nửa đường tròn (0) đường kính AB. Trên nửa đường tròn lấy 2 điểm C và D(D thuộc cung AC ) sao cho COD=90'. Các tia AD và BC cất nhau ở P, AC và BD cắt nhau ở H. a) Chứng minh tứ giác PDHC nội tiếp được trong đường tròn. b) Chứng minh APB = 45°. c) Gọi K là giao của PH với AB. Chứng minh PH.PK = PC.PB d) Chúng minh PH.PK = PO² -OB'