dựa vào đồ thị tốc độ chuyển động chúng ta có thể biết được điều gì

Những câu hỏi liên quan
Ta có thể dựa vào đồ thị (x – t) của dao động điều hòa để xác định vận tốc và gia tốc của vật được không?
Vì vận tốc tức thời được tính bằng công thức:
\(v=\dfrac{\Delta x}{\Delta t}\)
Và gia tốc tính bằng công thức:
\(a=\dfrac{\Delta x}{\Delta v}\)
Đúng 1
Bình luận (0)
( mọi người giúp mình với ạ, mình cảm ơn) Cho hai chuyển động thẳng có đô thị vận tốc. — thời gian của hai chất điểm (1) và (2), dựa vào đồ thị- Tinh chất chuyển động của mỗi chất điểm? Điểm A cho biết điều gì?- Tính gia tốc của mỗi chuyển động ( nếu có )- Hãy viết phương trình vận tốc và phương trình quãng đường của mỗi chất điểm- Quảng đường của chất điểm một sau 5s và trong giây thứ 5
Đọc tiếp
( mọi người giúp mình với ạ, mình cảm ơn)
Cho hai chuyển động thẳng có đô thị vận tốc. — thời gian của hai chất điểm (1) và (2), dựa vào đồ thị
- Tinh chất chuyển động của mỗi chất điểm? Điểm A cho biết điều gì?
- Tính gia tốc của mỗi chuyển động ( nếu có )
- Hãy viết phương trình vận tốc và phương trình quãng đường của mỗi chất điểm
- Quảng đường của chất điểm một sau 5s và trong giây thứ 5

Một vật chuyển động thẳng đều có đồ thị tọa độ theo thời gian như trên hình vẽ. Dựa vào đồ thị trên hãy cho biết vật chuyển động với vận tốc là bao nhiêu? A. 75m/s B. 50m/s C. 25m/s D. 150m/s
Đọc tiếp
Một vật chuyển động thẳng đều có đồ thị tọa độ theo thời gian như trên hình vẽ. Dựa vào đồ thị trên hãy cho biết vật chuyển động với vận tốc là bao nhiêu?
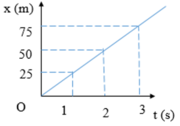
A. 75m/s
B. 50m/s
C. 25m/s
D. 150m/s
Đáp án C
- Áp dụng công thức:
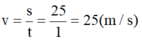
- Vận tốc của vật là 25 (m/s)
Đúng 0
Bình luận (0)
1. Hãy tính độ dịch chuyển của chuyển động có đồ thị (v-t) vẽ ở Hình 9.3b. Biết mỗi cạnh của ô vuông nhỏ trên trục tung ứng với 2 m/s, trên trục hoành ứng với 1 s.

2. Chứng tỏ rằng có thể xác định được giá trị của gia tốc dựa trên đồ thị (v - t).
1.
Độ dịch chuyển có độ lớn bằng diện tích của hình thang vuông có đường cao là t và các đáy có độ lớn v0, v.
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{v_0} = 4\left( {m/s} \right);v = 16\left( {m/s} \right)\\t = 6\left( s \right)\end{array} \right.\)
Suy ra: Độ dịch chuyển là:
\(d = \frac{{\left( {4 + 16} \right).6}}{2} = 60\left( m \right)\)
Đúng 0
Bình luận (0)
2.
Ta có: Gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
Từ đồ thị ta thấy: Độ biến thiên vận tốc các khoảng thời gian bằng nhau là 2 m/s.
Xét giữa 2 thời điểm A và B:
=> \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{{v_B} - {v_A}}}{{{t_A} - {t_B}}} = \frac{{12 - 10}}{{4 - 3}} = \frac{2}{1} = 2(m/{s^2})\)
Vậy có thể xác định được giá trị của gia tốc dựa trên đồ thị v – t.
Đúng 0
Bình luận (0)
. dựa vào đâu để ta so sánh chuyển động nào nhanh hơn chuyển động nào. . Độ lớn của vận tốc cho ta biết điều gì? . Giải một số bài tập ở SGK và sách bài tập về vận dụng công thức v để tính quãng đường .
Đọc tiếp
. dựa vào đâu để ta so sánh chuyển động nào nhanh hơn chuyển động nào.
. Độ lớn của vận tốc cho ta biết điều gì?
. Giải một số bài tập ở SGK và sách bài tập về vận dụng công thức v = để tính quãng đường .
a. Dựa vào đồ thị dưới đây và tính tốc độ của vật chuyển động trong khoảng thời gian đi 30 giây cuối cùng?b. Để đo độ sâu của biển người ta dùng sóng siêu âm. Thời gian khi phát ra âm đến khi nhận được âm phản xạ là 5 giây. Tính độ sâu của biển? Biết vận tốc truyền âm trong nước là 1500 m/s. c. Một người vũ công tập nhảy trước một gương phẳng. Hỏi nếu người đó di chuyển ra xa gương một khoảng 1,2 m thì ảnh của người đó cách người đó một khoảng bao nhiêu?
Đọc tiếp
a. Dựa vào đồ thị dưới đây và tính tốc độ của vật chuyển động trong khoảng thời gian đi 30 giây cuối cùng?
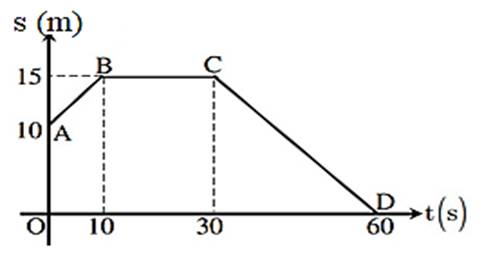
b. Để đo độ sâu của biển người ta dùng sóng siêu âm. Thời gian khi phát ra âm đến khi nhận được âm phản xạ là 5 giây. Tính độ sâu của biển? Biết vận tốc truyền âm trong nước là 1500 m/s.
c. Một người vũ công tập nhảy trước một gương phẳng. Hỏi nếu người đó di chuyển ra xa gương một khoảng 1,2 m thì ảnh của người đó cách người đó một khoảng bao nhiêu?
a. Dựa vào đồ thị dưới đây và tính tốc độ của vật chuyển động trong khoảng thời gian đi 30 giây cuối cùng?b. Để đo độ sâu của biển người ta dùng sóng siêu âm. Thời gian khi phát ra âm đến khi nhận được âm phản xạ là 5 giây. Tính độ sâu của biển? Biết vận tốc truyền âm trong nước là 1500 m/s. c. Một người vũ công tập nhảy trước một gương phẳng. Hỏi nếu người đó di chuyển ra xa gương một khoảng 1,2 m thì ảnh của người đó cách người đó một khoảng bao nhiêu?
Đọc tiếp
a. Dựa vào đồ thị dưới đây và tính tốc độ của vật chuyển động trong khoảng thời gian đi 30 giây cuối cùng?

b. Để đo độ sâu của biển người ta dùng sóng siêu âm. Thời gian khi phát ra âm đến khi nhận được âm phản xạ là 5 giây. Tính độ sâu của biển? Biết vận tốc truyền âm trong nước là 1500 m/s.
c. Một người vũ công tập nhảy trước một gương phẳng. Hỏi nếu người đó di chuyển ra xa gương một khoảng 1,2 m thì ảnh của người đó cách người đó một khoảng bao nhiêu?
vv
CẢNH BÁO! Tiếp tục đọc, hoặc linh hồn của bạn sẽ được thực hiện, ngay cả khi bạn đọc từ "cảnh báo"! Có một lần là một người tên là Duke Hunapon. Anh ta lười biếng, và rất bảnh bao. Anh ấy luôn mặc một chiếc áo khoác, không có vấn đề gì ở bên ngoài. Anh ta có một người anh trai tên là Michael, người luôn làm anh ta vây quanh. Một ngày nọ, Michael bị giết, và nó ảnh hưởng rất nhiều đến Duke. Anh ta phát điên và bắt đầu giết người. Chẳng mấy chốc, anh ta đã chiến đấu với ai đó và bị giết. Bây giờ, anh ta đi lang thang xung quanh như một bộ xương cao với một chiếc áo sơ mi màu đỏ, và cùng một chiếc áo hoodie mà Duke đã mặc. Bộ xương này được gọi là "Swapfell Papyrus", và anh ta sẽ giết bạn nếu bạn không đăng bài này trên 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ. Nếu bạn thất bại, và bạn thức dậy khi anh ta ở trong phòng của bạn, cái chết của bạn sẽ chậm và rất đau đớn. Một cô gái tên Lily Lilupanin đọc điều này, và không nghe. Cô bị hãm hiếp và bị giết trong giấc ngủ. Nếu bạn sao chép và dán vào 15 phần bình luận của bất kỳ trang web nào trước khi đi ngủ, Swapfell Papyrus sẽ đảm bảo bạn cảm thấy an toàn.Tôi là nạn nhân và tôi chỉ tình cờ đọc được bình luận này của 1 bạn khác khi đang xem 1 video. Tôi vốn không tin chuyện này nhưng vẫn làm đẻ đảm bảo tính mạng.Show less v
Đúng 0
Bình luận (0)
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t 0,2 s, độ dốc bằng 0 một lần nữa. Từ t 0,2 s đến t 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ -...
Đọc tiếp
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).
Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; …
Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.
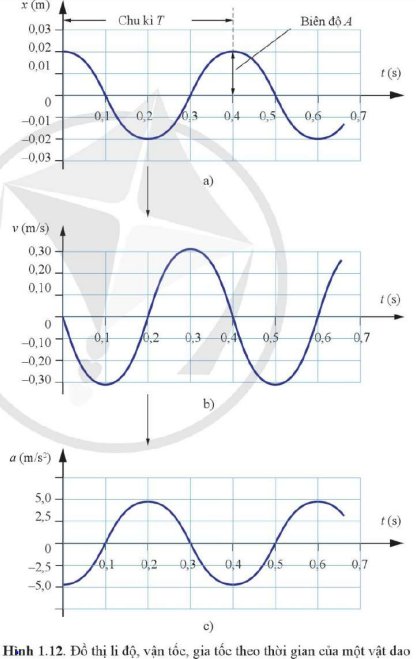
Dựa vào các đồ thị ở Hình `1.12` ta có:
- Các thời điểm gia tốc của xe bằng `0` là `t={0,1 ; 0,3 ; 0,5} (s)`
- Các thời điểm gia tốc của xe cực đại là `t={0 ; 0,2 ; 0,4 ; 0,6} (s)`
Cách làm: dựa vào đồ thị ở hình `c`, ta chiếu các thời điểm ứng với trục `t` sang trục `a`.
Đúng 1
Bình luận (0)
Trên hình 18 là đồ thị tọa độ - thời gian của ba vật chuyển động. Dựa vào đồ thị hãy:a) Cho biết các vật nào chuyển động cùng chiều và có vận tốc bằng nhau? Tại sao?b) Lập phương trình chuyển động của mỗi vật.c) Xác định vị trí và thời điểm các vật 2 và 3 gặp nhau. Kiểm tra lại bằng phép tính.
Đọc tiếp
Trên hình 18 là đồ thị tọa độ - thời gian của ba vật chuyển động. Dựa vào đồ thị hãy:
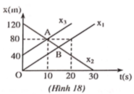
a) Cho biết các vật nào chuyển động cùng chiều và có vận tốc bằng nhau? Tại sao?
b) Lập phương trình chuyển động của mỗi vật.
c) Xác định vị trí và thời điểm các vật 2 và 3 gặp nhau. Kiểm tra lại bằng phép tính.
a) Vật 1 và vật 2 chuyển động cùng chiều và có vận tốc bằng nhau, vì đồ thị của chúng là hai đường thẳng song song nhau.
b) Phương trình chuyển động của các vật
Vật 1: x 1 = 4 t (m);
Vật 2: x 2 = 120 − 4 t (m);
Vật 3: x 3 = 40 + 4 t (m).
c) Vật 2 và vật 3 gặp nhau tại t = 10s, tọa độ x A = 80 m .
Đúng 0
Bình luận (0)
Dựa vào các đồ thị trong Hình 2.3:a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,5 s; 0,75 s và 1 sc) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
Đọc tiếp
Dựa vào các đồ thị trong Hình 2.3:
a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.
b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,5 s; 0,75 s và 1 s
c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
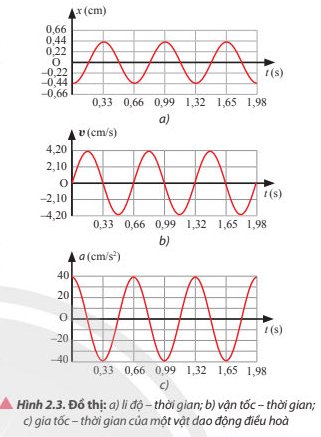
Biên độ dao động: A = 0,44 cm
Tốc độ cực đại: vmax = 4,2 cm/s
Gia tốc cực đại: amax = 40 cm/s2
Chu kì của gia tốc của vật: T = 0,66 s.
Tốc độ góc: \(\omega = \frac{{2\pi }}{T} = \frac{{100}}{{33}}\pi (rad/s)\)
a) Tại thời điểm ban đầu vật đi từ biên âm tiến về VTCB nên pha ban đầu φ0 = π(rad)
Khi đó, phương trình li độ có dạng:
x = Acos(ωt+φ0) = 0,44cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm)
Phương trình vận tốc có dạng:
v = ωAcos(ωt+φ0+\(\frac{\pi }{2}\)) = 4,2cos(\(\frac{{100\pi }}{{33}}\)t+\(\frac{{3\pi }}{2}\)) (cm/s)
Phương trình gia tốc có dạng:
a = −ω2Acos(ωt+φ0) = −40cos(\(\frac{{100\pi }}{{33}}\)t+π) (cm/s2)
b)
Từ đồ thị có thể thấy:
t= 0,33s: x=0,44 cm; v=0 cm/s; a=-40 cm/s2
t= 0,495s: x=0 cm; v=-4,2 cm/s; a=0 cm/s2
t= 0,66s: x=-0,44 cm; v=0 cm/s; a=40 cm/s2
c) Nghiệm lại với các phương trình.
- Tại thời điểm t = 0,5 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = −0,02 (cm)
v =4,2cos(\(\frac{{100\pi }}{{33}}\).0,5+3π2) = −4,19 (cm/s)
a =−40cos(\(\frac{{100\pi }}{{33}}\).0,5+π) = 1,9 (cm/s2)
- Tại thời điểm t = 0,75 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = −0,29 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).0,75+\(\frac{{3\pi }}{2}\)) = 3,17 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).0,75+π) = 26,2 (cm/s2)
- Tại thời điểm t = 1 s
x = 0,44cos(\(\frac{{100\pi }}{{33}}\).1+π) = 0,438 (cm)
v = 4,2cos(\(\frac{{100\pi }}{{33}}\).1+3π2) = −0,4 (cm/s)
a = −40cos(\(\frac{{100\pi }}{{33}}\).1+π) = −39,8 (cm/s2)
Đúng 0
Bình luận (0)















