lập bảng biến thiên y=|2x-7|

Những câu hỏi liên quan
Khảo sát sự biến thiên và lập bảng biến thiên của hàm số :
y = x2 + 2x -2 trên ( -∞;1), (-1;+∞)
\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-x_2^2-2x_2+2}{x_1-x_2}\)
\(=\left(x_1+x_2\right)-2\)
Vì \(x_1;x_2\in\left(-\infty;1\right)\) thì \(\left\{{}\begin{matrix}x_1< 1\\x_2< 1\end{matrix}\right.\Leftrightarrow\left(x_1+x_2\right)< 2\)
\(\Leftrightarrow\left(x_1+x_2\right)-2< 0\)
Vậy: Hàm số nghịch biến trên \(\left(-\infty;1\right)\)
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ (P): y = -x2 - 2x + 3
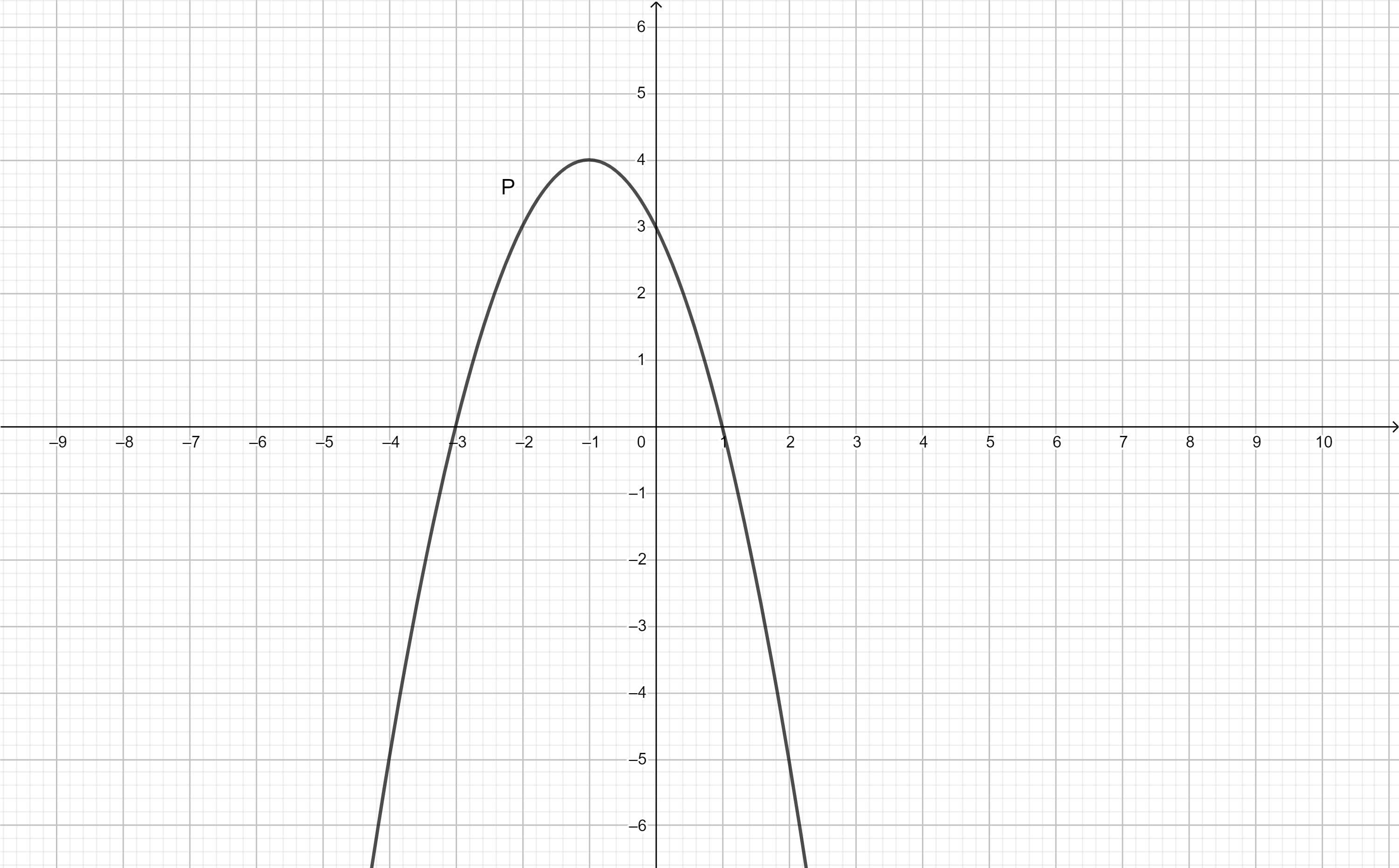
e học lp 9 nên k bic lập bảng biến thiên ạ 🙁
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ y=-2x^2+3x-1
| x | -∞ | \(\dfrac{3}{4}\) | +∞ |
| y | -∞ | \(\dfrac{1}{8}\) | -∞ |
Đúng 0
Bình luận (0)
Lập bảng biến thiên của hàm số y=x^2+2x-3
Lập bảng biến thiên và vẽ đồ thị của mỗi hàm số
y = | 2 x - 3 |
Ta có thể viết

Từ đó có bảng biến thiên và đồ thị của hàm số
y = |2x - 3| (h.32)
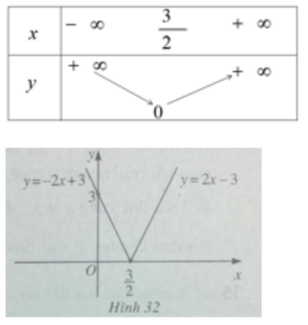
Đúng 0
Bình luận (0)
Cho pt : x^2-2x-7-4m (1)Lập bảng biến thiên của pt bậc 2 : x^2-2x-7. Nhìn vào bảng biến thiên hãy tìm m để pt (1):a. Có 1 nghiệm duy nhất trên đoạn left[-2;2right], trên đoạn left[2;3right], trên đoạn left[-2;-1right]b. Có 2 nghiệm pb trên đoạn left[-2;2right], left[2;3right],left[-2;-1right] c. Có nghiệm trên đoạn left[-2;2right], left[2;3right],left[-2;-1right]d. Có 2 nghiệm trên đoạn left[-2;2right],left[2;3right],left[-2;-1right]e. Vô nghiệm trên đoạn left[-2;2right], left[2;3right],left[-2;...
Đọc tiếp
Cho pt : \(x^2-2x-7=-4m\) (1)
Lập bảng biến thiên của pt bậc 2 : \(x^2-2x-7\). Nhìn vào bảng biến thiên hãy tìm m để pt (1):
a. Có 1 nghiệm duy nhất trên đoạn \(\left[-2;2\right]\), trên đoạn \(\left[2;3\right]\), trên đoạn \(\left[-2;-1\right]\)
b. Có 2 nghiệm pb trên đoạn \(\left[-2;2\right]\), \(\left[2;3\right],\left[-2;-1\right]\)
c. Có nghiệm trên đoạn \(\left[-2;2\right]\), \(\left[2;3\right],\left[-2;-1\right]\)
d. Có 2 nghiệm trên đoạn \(\left[-2;2\right]\),\(\left[2;3\right],\left[-2;-1\right]\)
e. Vô nghiệm trên đoạn \(\left[-2;2\right]\), \(\left[2;3\right],\left[-2;-1\right]\)
Giups mk bài này vs . Mk đg cần gấp . Tks ạ
a, (1) có nghiệm duy nhất trên [-2 ; 2] khi
[-2 ; 2] khi \(\left[{}\begin{matrix}-4m=-8\\1\ge-4m>-7\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}m=2\\\dfrac{-1}{4}\le m< \dfrac{7}{4}\end{matrix}\right.\) hay m ϵ [\(\dfrac{-1}{4};\dfrac{7}{4}\)) \(\cup\left\{2\right\}\)
(1) có nghiệm duy nhất trên [2 ; 3] khi
- 4 ≥ - 4m ≥ - 7 ⇔ 1 ≤ m ≤ \(\dfrac{7}{4}\) hay m ∈\(\left[1;\dfrac{7}{4}\right]\)
(1) có nghiệm duy nhất trên [-2; -1] khi
-4 ≤ 4m ≤ 1 hay m ∈ \(\left[\dfrac{-1}{4};1\right]\)
b, (1) có 2 nghiệm phân biệt trên [-2 ; 2] khi
-4m ∈ (-8 ; -7] ⇒ m ∈\(\)[\(\dfrac{7}{4}\); 2)
(1) có 2 nghiệm phân biệt trên [2; 3] và [-2; -1] khi m ∈ ∅
c, (1) có nghiệm trên đoạn
[-2; 2] khi -8 ≤ -4m ≤ 1 ⇒ m ∈ \(\left[\dfrac{-1}{4};2\right]\)
[2 ; 3] khi - 4 ≥ - 4m ≥ - 7 hay m ∈\(\left[1;\dfrac{7}{4}\right]\)
[-2 ; -1] khi -4 ≤ 4m ≤ 1 hay m ∈ \(\left[\dfrac{-1}{4};1\right]\)
d, dường như là nó giống câu b,
e, (1) vô nghiệm trên đoạn [-2 ; 2] khi
\(\left[{}\begin{matrix}-4m>1\\-4m< -8\end{matrix}\right.\)hay \(m\in\left(-\infty;\dfrac{-1}{4}\right)\cup\left(2;+\infty\right)\)
(1) vô nghiệm trên đoạn [2; 3] khi
m ∈ R \ \(\left[1;\dfrac{7}{4}\right]\)
(1) vô nghiệm trên [-2 ; -1] khi m ∈ R \ \(\left[\dfrac{-1}{4};1\right]\)
Có sai sót xin thông cảm
P/s :Bạn tự vẽ bảng biến thiên nha, nhớ chia khoảng cách các giá trị của x cho chuẩn vào, nhớ thêm cả f(0) và trong bảng nhá
Đúng 1
Bình luận (1)
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = -3x2 + 2x - 1
y = –3x2 + 2x – 1.
+ Tập xác định: R
+ Đỉnh A(1/3 ; –2/3).
+ Trục đối xứng x = 1/3.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung là B(0; –1).
Điểm đối xứng với B(0 ; –1) qua đường thẳng x = 1/3 là C(2/3 ; –1).
+ Bảng biến thiên:
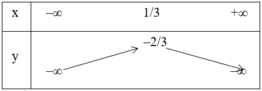
+ Đồ thị hàm số :
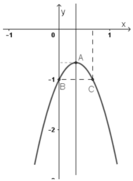
Đúng 0
Bình luận (0)
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = x2 - 2x - 1
Hàm số y = x2 – 2x – 1 có a = 1 > 0 ; b = –2 ; c = –1:
+ Tập xác định D = R.
+ Nghịch biến trên (–∞ ; 1) ; đồng biến trên (1 ; + ∞).
Bảng biến thiên:
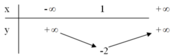
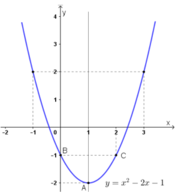
+ Đồ thị hàm số là parabol có:
Đỉnh A(1 ; –2)
Trục đối xứng là đường thẳng x = 1.
Giao điểm với Oy tại B(0 ; –1). Điểm đối xứng với B qua đường thẳng x = 1 là C(2 ; –1).
Đi qua các điểm (3 ; 2) và (–1 ; 2).
Đúng 0
Bình luận (0)
lập bảng biến thiên và vẽ đồ thị của hàm số y=x^2 - 2x +1( Giải giúp e với)
xét sự biến thiên của hàm số sau trên tập xác định của nó và lập bảng biến thiên:
a, \(y=-x^2-2x+3\)
b, \(y=\dfrac{x+1}{x-2}\)
a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Đúng 0
Bình luận (1)
















