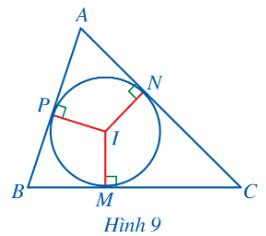
Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).
Những câu hỏi liên quan
Cho tam giác ABC có AB=8,AC=6,BC=10.Vẽ đường tròn(C;CA)
a) Chứng minh AB là tiếp tuyến của đường tròn(C)
b) Xác vị trí tương đối của đường thẳng BC với đường tròn(C)
a) Xét tam giác ABC có:
\(AB^2+AC^2=8^2+6^2=100=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow AB\perp AC\)
Mà \(A\in\left(C;CA\right)\)
=> AB là tiếp tuyến đường tròn (C)
b) Ta có: AB là tiếp tuyến, C là tâm
=> BC cắt đường tròn
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn có đường cao CI .gọi H và K lần lượt là hình chiếu của I Trên BC và AC a Chứng minh 4 điểm I H C K thuộc một đường tròn b nêu vị trí của đường thẳng AB với đường tròn trên c 1 đường thẳng đi qua trung điểm của CI và vuông góc với IK cắt AB ở E . chứng minh EK là tiếp tuyến của đường tròn trên
Xem chi tiết
a:
Gọi O là trung điểm của CI
Xét tứ giác CKIH có
\(\widehat{CKI}+\widehat{CHI}=90^0+90^0=180^0\)
=>CKIH là tứ giác nội tiếp đường tròn đường kính CI
=>C,K,H,I cùng thuộc (O)
b: Xét (O) có
OI là bán kính
AB\(\perp\)OI tại I
Do đó; AB là tiếp tuyến của (O)
c: Ta có: ΔOKI cân tại O
mà OE là đường cao
nên OE là phân giác của góc KOI
Xét ΔOKE và ΔOIE có
OK=OI
\(\widehat{KOE}=\widehat{IOE}\)
OE chung
Do đó: ΔOKE=ΔOIE
=>\(\widehat{OKE}=\widehat{OIE}\)
=>\(\widehat{OKE}=90^0\)
=>EK là tiếp tuyến của (O)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=3cm;AC=4cm. Vẽ đường tròn(A ; 2,8cm). Xác định vị trí tương đối của đường thẳng BC và đường tròn(A ; 2,8cm)
Cho tam giác ABC có đường cao AH, nội tiếp trong đường tròn tâm O, đường kính BC. Gọi E,D lần lượt là hình chiếu của H trên cạnh AB, AC.a/ CMR: tứ giác ADHE là hình chữ nhậtb/ Chứng minh AB.AEAD.ACc/ Gọi I,J lần lượt k là tâm các đường tròn ngoại tiếp tam giác CDH,BEH.Xác định vị trí tương đối giữa các đường tròn (i) và (J) và (O)d/ CMR: ID là tiếp tuyến của đường tròn ngoại tiếp tam giác AEH.
Đọc tiếp
Cho tam giác ABC có đường cao AH, nội tiếp trong đường tròn tâm O, đường kính BC. Gọi E,D lần lượt là hình chiếu của H trên cạnh AB, AC.
a/ CMR: tứ giác ADHE là hình chữ nhật
b/ Chứng minh AB.AE=AD.AC
c/ Gọi I,J lần lượt k là tâm các đường tròn ngoại tiếp tam giác CDH,BEH.Xác định vị trí tương đối giữa các đường tròn (i) và (J) và (O)
d/ CMR: ID là tiếp tuyến của đường tròn ngoại tiếp tam giác AEH.
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi A1,B1,C1 tương ứng là tiếp điểm của (I) với các cạnh BC,CA,AB. Các đường tròn ngoại tiếp các tam giác BC1B1,CB1C1 tương ứng cắt lại đường thẳng BC tại điểm K (khác B) và tại điểm L (khácC). Chứng minh rằng các đường thẳng LC1,KB1 và IA1 đồng quy.
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).
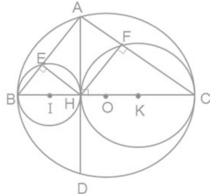
IO = OB – IB => (I) tiếp xúc trong với (O).
OK = OC – KC => (K) tiếp xúc trong với (O)
IK = OH + KH => (I) tiếp xúc ngoài với (K)
Đúng 0
Bình luận (0)
ai giúp em với ạ 5h em đi học thêm rồi !-cho tam giác ABC vuông tại A, đường cao AH . Vẽ đường tròn (O), (I) ,(K) có các đường kính lần lượt là BC, CH, BHa)Hãy xác định vị trí tương đối của (I),(O) và (K)b) AC cắt đường tròn (I) tại D , AB cắt đường tròn (K) tại E. Chứng minh DE là tiếp tuyến chung của hai đường tròn (I) vả (K)c)Xác định vị trí của H ở trên đường kính BC sao cho ED có độ dài lớn nhấtd)Tam giác ABC phải có thêm điều kiện gì để HB + HC + 2DE
Đọc tiếp
ai giúp em với ạ 5h em đi học thêm rồi !
-cho tam giác ABC vuông tại A, đường cao AH . Vẽ đường tròn (O), (I) ,(K) có các đường kính lần lượt là BC, CH, BH
a)Hãy xác định vị trí tương đối của (I),(O) và (K)
b) AC cắt đường tròn (I) tại D , AB cắt đường tròn (K) tại E. Chứng minh DE là tiếp tuyến chung của hai đường tròn (I) vả (K)
c)Xác định vị trí của H ở trên đường kính BC sao cho ED có độ dài lớn nhất
d)Tam giác ABC phải có thêm điều kiện gì để HB + HC + 2DE
Cho tam giác ABC vuông tại A có AB=3cm, AC=4cm. Vẽ đường tròn tâm A bán kính 2,8cm. Hãy xác định vị trí tương đối của đường thẳng BC và đường tròn (A;2,8)
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.a) Tứ giác MNCB là hình gì ?b) CM: AM.AN MB.NCc) CM: tam giác OMN là tam giác când) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
Đọc tiếp
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.
a) Tứ giác MNCB là hình gì ?
b) CM: AM.AN = MB.NC
c) CM: tam giác OMN là tam giác cân
d) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.a) Tứ giác MNCB là hình gì ?b) CM: AM.AN MB.NCc) CM: tam giác OMN là tam giác când) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.
Đọc tiếp
Cho nửa đường tròn (O;R), đường kính BC và điểm A thuộc nửa đường tròn đó. Dựng về phía ngoài tam giác ABC hai nửa đường tròn: nửa đường tròn tâm I, đường kính AB; nửa đường tròn tâm K đường kính AC. Một đường thẳng d thay đổi qua A cắt nửa đường tròn (I) và (K) tương ứng tại M và N.
a) Tứ giác MNCB là hình gì ?
b) CM: AM.AN = MB.NC
c) CM: tam giác OMN là tam giác cân
d) Xác định vị trí của đường thẳng d để diện tích tứ giác BMNC lớn nhất.