Biểu diễn số hữu tỉ sau dưới dạng liên phân số hữu hạn: 38/117
Những câu hỏi liên quan
Chỉ ra các khẳng định nào sau đây đúng :
A. Mỗi số thực đều biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
B. Các điểm biểu diễn số hữu tỉ lấp đầy trục số.
C. Nếu a là số hữu tỉ thì a cũng là số thực.
D. Các bình phương của hai số thực đối nhau là hai số đối nhau.
Câu 1: Trong các khẳng định sau, khẳng định nào là sai:A.Nếu a là số thực thì a biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn B.Mỗi số thực được biểu diễn bởi nhiều điểm trên trục số C.Số hữu tỉ và số vô tỉ được gọi chung là số thực.Tập hợp các số thực được kí hiệu là RD.Mỗi điểm trên trục số biểu diễn một số thực Câu 2:Khẳng định nào dưới đây là sai :A.Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoànB.Số vô tỉ là số viết dưới dạng số thập phân hữu hạn C.Số dương khôn...
Đọc tiếp
Câu 1: Trong các khẳng định sau, khẳng định nào là sai:
A.Nếu a là số thực thì a biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn
B.Mỗi số thực được biểu diễn bởi nhiều điểm trên trục số
C.Số hữu tỉ và số vô tỉ được gọi chung là số thực.Tập hợp các số thực được kí hiệu là R
D.Mỗi điểm trên trục số biểu diễn một số thực
Câu 2:Khẳng định nào dưới đây là sai :
A.Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn
B.Số vô tỉ là số viết dưới dạng số thập phân hữu hạn
C.Số dương không có hai căn bậc hai là hai số đối nhau
D.Số âm không có căn bậc hai
a) Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân:frac{{15}}{8};,,,frac{{ - 99}}{{20}};,,,frac{{40}}{9};,,, - frac{{44}}{7}b) Trong các số thập phân vừa tính được, hãy chỉ ra các số thập phân vô hạn tuần hoàn.
Đọc tiếp
a) Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân:
\(\frac{{15}}{8};\,\,\,\frac{{ - 99}}{{20}};\,\,\,\frac{{40}}{9};\,\,\, - \frac{{44}}{7}\)
b) Trong các số thập phân vừa tính được, hãy chỉ ra các số thập phân vô hạn tuần hoàn.
a)\(\frac{{15}}{8} = 1,875;\,\,\,\,\,\,\,\frac{{ - 99}}{{20}} = - 4,95;\,\,\,\,\,\,\\\frac{{40}}{9} = 4,\left( 4 \right);\,\,\, - \frac{{44}}{7} = - 6,(285714)\)
b) Trong các số thập phân trên, số thập phân 4,(4) và -6,(285714) là các số thập phân vô hạn tuần hoàn với chu kì lần lượt là 4 và 285714
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 17:57
Ta biết rằng, sqrt 2 là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: sqrt 2 1,414213562...Cũng có thể coi sqrt 2 là giới hạn của dãy số hữu tỉ left( {{r_n}} right):1,4;1,41;1,414;1,4142;...Từ đây, ta lập dãy số các luỹ thừa left( {{3^{{r_n}}}} right).a) Bảng dưới cho biết những số hạng đầu tiên của dãy số left( {{3^{{r_n}}}} right) (làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.
Đọc tiếp
Ta biết rằng, \(\sqrt 2 \) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2 = 1,414213562...\)
Cũng có thể coi \(\sqrt 2 \) là giới hạn của dãy số hữu tỉ \(\left( {{r_n}} \right)\):
\(1,4;1,41;1,414;1,4142;...\)
Từ đây, ta lập dãy số các luỹ thừa \(\left( {{3^{{r_n}}}} \right)\).
a) Bảng dưới cho biết những số hạng đầu tiên của dãy số \(\left( {{3^{{r_n}}}} \right)\) (làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.
a: \(r_6=3^{\text{1 , 414213 }}=4,7288\text{01466}\)
\(r_7=3^{\text{ 1 , 4142134}}=\text{4,728803544}\)
b: Khi \(n\rightarrow+\infty\) thì \(3^{r_n}\rightarrow3^{\sqrt{2}}\)
Đúng 0
Bình luận (0)
Giải thích vì sao các phân số sau viết dưới dạng số thập phân hữu hạn rồi viết chúng dưới dạng đó:
3 8 ; - 7 5 ; 13 20 ; - 13 125
+ 8 = 23 chỉ có ước nguyên tố là 2
⇒ 
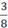viết được dưới dạng số thập phân hữu hạn. 
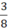= 0,375
+ 5 chỉ có ước nguyên tố là 5
⇒ 
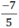viết được dưới dạng số thập phân hữu hạn. 
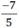= -1,4
+ 20 = 22.5 có ước nguyên tố là 2 và 5.
⇒ 
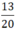viết được dưới dạng số thập phân hữu hạn. 
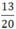= 0,65
+ 125 = 53 chỉ có ước nguyên tố là 5.
⇒ 
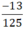viết được dưới dạng số thập phân hữu hạn. 
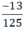= -0,104
Đúng 0
Bình luận (0)
Trong các khẳng sau, khẳng định nào sai?A. Mỗi số thạp phân vô hạn tuần hoàn đều là số hữa tỉ.B. Mỗi số thập phân hữu hạn đều là một số hữu tỉ.C. Mỗi số hữu tỉ đều được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoànD. Một phân số có mẫu dương mà mẫu có ước nguyên tố khác và thì phân số đó được viết dưới dạng số thập phân hữu hạn.
Đọc tiếp
Trong các khẳng sau, khẳng định nào sai?
A. Mỗi số thạp phân vô hạn tuần hoàn đều là số hữa tỉ.
B. Mỗi số thập phân hữu hạn đều là một số hữu tỉ.
C. Mỗi số hữu tỉ đều được biểu diễn bởi một số thập phân hữu hạn hoặc vô hạn tuần hoàn
D. Một phân số có mẫu dương mà mẫu có ước nguyên tố khác và thì phân số đó được viết dưới dạng số thập phân hữu hạn.
Một phân số có mẫu dương mà mẫu có ước nguyên tố khác gì và gì thì phân số đó được viết dưới dạng số thập phân hữu hạn hả bạn
Đúng 1
Bình luận (0)
D
Nghĩ là z (vì bn ghi ko rõ nên mik ko hiểu) tại mấy câu kia đúng
Đúng 1
Bình luận (0)
Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân: \(\frac{{12}}{{25}};\frac{{27}}{2};\frac{{10}}{9}\)
\(\frac{{12}}{{25}} = 0,48;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{27}}{2} = 13,5;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{10}}{9} = 1,(1)\)
Đúng 0
Bình luận (0)
Thực hành 1: Hãy biểu diễn các số hữu tỉ sau đây dưới dạng số thập phân: 12/25; 27/2; 10/9
\(\dfrac{12}{25}=\dfrac{12\times4}{25\times4}=\dfrac{48}{100}=0,48\)
\(\dfrac{27}{2}=\dfrac{27\times5}{2\times5}=\dfrac{135}{10}=13,5\)
\(\dfrac{10}{9}=1+\dfrac{1}{9}=1+0,\left(1\right)=1,\left(1\right)=1,111...\)
Đúng 1
Bình luận (0)
nêu hai khả năng khi biểu diễn mọt số hữu tỉ dưới dạng số thập phân. đỊNH NGHĨA SỐ VÔ TỈ