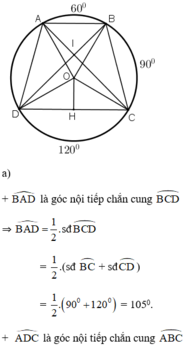
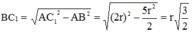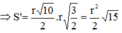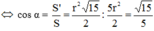Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r) sao cho điểm M nằm trong hình vuông ABCD. Tiếp tuyến của đường tròn (C; r) tại tiếp điểm M cắt các đoạn thẳng AB, AD lần lượt tại N, P. Chứng minh:
a) Các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r).
b) \(\widehat{NPC}=\widehat{NCB}+\widehat{PCD}=45^o\).