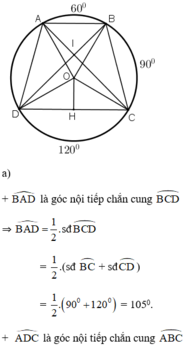
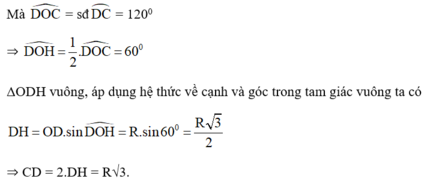Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho
sd A B ^ = 60 ° , sd B C ^ = 90 ° và sd C D ^ = 120 °
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R.
b)
Gọi AC giao DB = I
Góc AIB có đỉnh I nằm trong đường tròn
\(\Rightarrow\widehat{AIB}=\frac{1}{2}.\left(sđ\widebat{AB}+sđ\widebat{CD}\right)\)
\(=\frac{1}{2}.\left(60^0+90^o\right)=90^o\)
=> AI vuông BI hay AC vuông BD ( đpcm )
c)
+) Tam giác OAB có :
OA = OB ; \(\widehat{AOB}=sđ\widebat{AB}=60^o\)
=> Tam giác OAB đều
=> AB = OA = OB = R
+) Tam giác OBC có \(\widehat{BOC}=sđ\widebat{BC}=90^o;OB=OC=R\)
- Áp dụng đlí Py - ta - go cho OBC , ta có :
\(BC^2=OB^2+OC^2=R^2+R^2=2R^2\)
\(\Rightarrow BC=R\sqrt{2}\)
+) ABCD là hình thang cân
\(\Rightarrow AD=BC=R\sqrt{2}\)
+) Gọi H là trung điểm của CD
Ta có : OD = OC
=> Tam giác OCD cân tại O
=> OH đồng thời là đường cao vừa là đường phân giác
Mà \(\widehat{DOC}=sđ\widebat{DC}=120^o\)
\(\Rightarrow\widehat{DOH}=\frac{1}{2}.\widehat{DOC}=60^o\)
Tam giác ODH vuông , áp dụng hệ thức về cạnh trong tam giác vuông , ta có :
\(DH=OD.\sin\widehat{DOH}=R.sin60^o=\frac{R\sqrt{3}}{2}\)
\(\Rightarrow CD=2.DH=R\sqrt{3}\)