+ ∆ O A B có

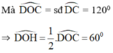
∆ O D H vuông, áp dụng hệ thức về cạn và góc trong tam giác vuông ta có
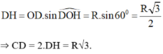

+ ∆ O A B có

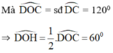
∆ O D H vuông, áp dụng hệ thức về cạn và góc trong tam giác vuông ta có
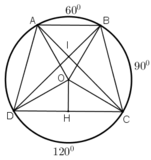
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho sđ A B ⏜ = 60 o , sđ B C ⏜ = 90 o , sđ C D ⏜ = 120 o
Tứ giác ABCD là hình gì?
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho sđ A B ⏜ = 60 o , sđ B C ⏜ = 90 o , sđ C D ⏜ = 120 o
Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho
sd A B ^ = 60 ° , sd B C ^ = 90 ° và sd C D ^ = 120 °
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R.
Tren đtr o bk r. Lấy day ab=R sđ cung AC bằng 90 sao cho AB,AC nằm cùng phía với AO.
a) tính AC theo R. Tính sđ bc
b) gọi AH là đường cao của tam giác ABC tính độ dài HA ,HB theo R
c) tính theo R phần diện tích tam giác ABH ở ngoài hình tròn o
Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D . a) Tính sđ góc BOC và sđ cung nhỏ AC . b) chứng minh tứ giác OBDC nội tiếp . c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE . d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ ∠ BC = 1 6 sđ ∠ BA; sđ ∠ BD = 1 2 sđ ∠ BA; sđ ∠ BE = 2 3 sđ ∠ BA. So sánh hai cung nhỏ AE và BC.
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ ∠ BC = 1 6 sđ ∠ BA; sđ ∠ BD = 1 2 sđ ∠ BA; sđ ∠ BE = 2 3 sđ ∠ BA. Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ ∠ BC = 1 6 sđ ∠ BA; sđ ∠ BD = 1 2 sđ ∠ BA; sđ ∠ BE = 2 3 sđ ∠ BA. Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 180 ° ).
BT1: Trên đường tròn (O; R) lấy A,B,C sao cho dây AC=R, dây BC= R √ 2, tia CO nằm giữa tia CA và CB. Tính sđ các GÓC: AOC, COB, AOB. Tính sđ cung BC
BT2: Cho tam giác ABC cân tại A, góc A nhọn. Đường tròn (O), đường kính BC cắt AB, AC tại D và E.
CM: BE = CD ⇒ góc BDE = góc DEC.
CM: cung CE = cung BD