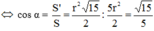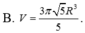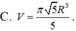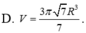Question

Cho hình trụ có bán kính r và có chiều cao cũng bằng r. Hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.

Answer 1

Gọi  C C 1 và  D D 1 là hai đường sinh của khối trụ

Khi đó  D 1 C 1 / / = D C (1)

Đông thời ABCD là hình vuông nên AB//=DC (2)

Từ (1) và (2) suy ra AB//= D 1 C 1

Vậy  A B C 1 D 1 nội tiếp đường tròn (O) nên  A B C 1 D 1 là hình chữ nhật. Suy ra  A C 1 là đường kính của (O)

Nghĩa là  A C 1 = 2 r

Tam giác  A B C 1 vuông ở B nên:

(3)

Tam giác  B C C 1 vuông ở  C 1 nên:

(4)

Từ (3) và (4) suy ra 

Vậy diện tích hình vuông ABCD là  S = A B 2 = 5 r 2 2

* Gọi  α là góc hợp bởi mp(ABCD) và mặt phẳng đáy của hình trụ, ta có:

Với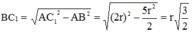 

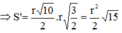
Mà  A B C 1 D 1 là hình chiếu của ABCD trên mặt đáy hình trụ nên:

S ' = S . cos α