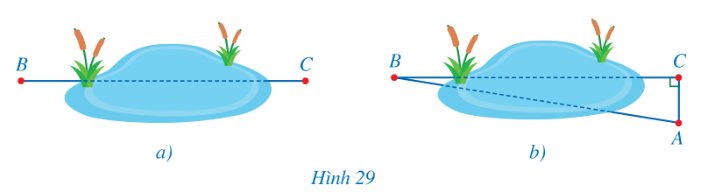
Hãy giải bài toán ở phần mở đầu và tính AB trong Hình 29b (làm tròn kết quả đến hàng phần trăm của mét).
Trong bài toán ở phần mở đầu, độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
- Cách 1:
Hàm số biểu diễn đồ thị \(y = - 0,00188{\left( {x - 251,5} \right)^2} + 118\)
\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)
Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)
- Cách 2:
Ta có phương trình thành cầu: \(y = – 0,00188(x – 251,5)^2 + 118\)
\( \Leftrightarrow y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai.
Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I.
Ta có: \(b = 0,94564, c = – 0,91423\)
\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I = – 0,00188(x_I – 251,5)^2 + 118 =118.\)
Vậy độ cao lớn nhất cần tìm là 118 m.
Em hãy đọc đoạn tin ngắn ở phần mở đầu rồi làm tròn số 479 633 tới hàng nghìn và làm tròn số 232,142 372 tới hàng đơn vị. So sánh hai kết quả với các số liệu trong tiêu đề của đoạn tin đó.

+) Làm tròn số 479 633 tới hàng nghìn :
Chữ số ở hàng làm tròn là chữ số 9.
Chữ số ngay bên phải hàng làm tròn là 6 > 5 nên ta tăng chữ số hàng làm tròn thêm 1 đơn vị; các chữ số sau hàng làm tròn thuộc phần số nguyên nên ta thay bằng chữ số 0 . Khi đó ta được số làm tròn là: 480 000.
+) Làm tròn số 232,142 372 tới hàng đơn vị:
Chữ số ở hàng làm tròn là chữ số 2.
Chữ số ngay bên phải hàng làm tròn là 1 < 5 nên ta giữ nguyên chữ số ở hàng làm tròn; các chữ số sau hàng làm tròn thuộc phần thập phân nên ta bỏ đi hết . Khi đó ta được số làm tròn là: 232.
Giải bài toán tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).
Từ 2020 đến 2050 sẽ là 2050-2020=30(năm)
Dân số VN vào năm 2050 sẽ là:
\(97.34\cdot e^{0.91\%\cdot30}\simeq127,90\)(triệu người)
Làm tròn kết quả của phép tính sau đến hàng phần trăm: 4,8 : 2,56
4,8 ÷ 2,56 = 1,875 = 1,88
Chúc bạn học tốt
Bài 2 (1 điểm) Thực hiện phép tính rồi làm tròn kết quả đến hàng phần trăm. a) 0,756 + 4,843 b) 0,432.10 + 3,413.10
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính \(\sin \alpha \) và \(\cos \alpha \), từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
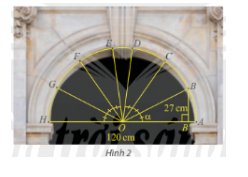
Ta có: \(OA = OB = 120:2 = 60\)
Xét tam giác OBB’ có:
\(\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\)
\(\widehat {AOC} = 2\widehat {BOB'}\)
(Vì số đo cung AC gấp 2 lần số đo cung AB)
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}\)
Mà \(\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}\)
\( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\)
Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).
chu vi tam giác đều = 20 cm. tính độ dài cạch của tam giác (làm tròn đến kết quả đến hàng phần trăm)
Độ dài cạnh của tam giác là:
\(\dfrac{20}{3}\simeq6,67\left(cm\right)\)
Thực hiện phép tính rồi làm tròn kết quả đến hàng phần trăm :
a, 0,756 + 4,843
b, 0,432 x 10 + 3,413 x 10
Giải nhanh giúp em vs ạ
a: =5,599=5,60
b: =10(0,432+3,413)=10x3,845=38,45=38,50
Một bánh xe hình tròn có đường kính là 700 mm chuyển động trên một đường thẳng từ điểm A đến điểm B sau 875 vòng. Quãng đường AB dài khoảng bao nhiêu ki-lô-mét (làm tròn kết quả đến hàng phần mười và lấy π = 3,14)?
mình nhầm bạn ơi,phải là 3,142 mới đúng nhé:((