Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):
a) 41°; b) 28°35’; c) 70°27’46’’.
Những câu hỏi liên quan
Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.
a) 3; b) 41; c) 2 021
Làm tròn các kết quả với độ chính xác 0,005 tức là làm tròn đến hàng phần trăm.
\(\begin{array}{l}a)\sqrt 3 = 1,73205.... \approx 1,73\\b)\sqrt {41} = 6,40312.... \approx 6,40\\c)\sqrt {2021} = 44,95553.... \approx 44,96\end{array}\)
Đúng 0
Bình luận (0)
Làm tròn các số với độ chính xác 0,005 đc kết quả là:
a)√3=1,73205....≈1,73
b)√41=6,40312....≈6,40
c)√2021=44,95553....≈44,96
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:07
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):
a) \({\log _5}0,5\);
b) \(\log 25\);
c) \(\ln \frac{3}{2}\).
a) \(log_50,5=-0,439677\)
c) \(In\left(\dfrac{3}{2}\right)=0,405465\)
Đúng 1
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 18:14
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư):
a) \({\log _3}15\);
b) \(\log 8 - \log 3\);
c) \(3\ln 2\).
a) \(log_315=2,4650\)
c) \(3In2=2,0794\)
Đúng 2
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
18 tháng 8 2023 lúc 17:58
a) Sử dụng máy tính cầm tay, hoàn thành bảng sau vào vở (làm tròn kết quả đến chữ số thập phân thứ năm).
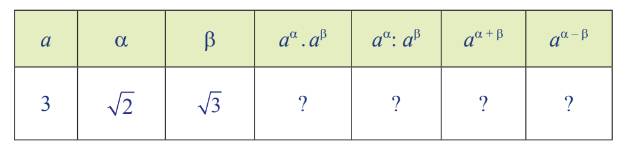
b) Từ kết quả quả ở câu a, có dự đoán gì về tính chất của phép tính luỹ thừa với số mũ thực?
a)
| a | α | b | \(a^{\alpha}\cdot a^{\beta}\) | \(a^{\alpha}:a^{\beta}\) | \(a^{\alpha+\beta}\) | \(\alpha^{\alpha+\beta}\) |
| 3 | \(\sqrt{2}\) | \(\sqrt{3}\) | \(3^{\sqrt{2}}\cdot3^{\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}}:3^{\sqrt{3}}=0,70527\) | \(3^{\sqrt{2}+\sqrt{3}}=31,70659\) | \(3^{\sqrt{2}-\sqrt{3}}=0,70527\) |
b) Nhận xét:
\(a^m\cdot a^n=a^{m+n};a^m:a^n=a^{m-n}\)
Đúng 1
Bình luận (0)
Dùng máy tính cầm tay để A) tính độ dài cạnh của một miếng đất hình vuông có S=12 996m² B) Tính bán kính của 1 hình tròn có S=100 cm²(làm tròn kết quả đến hàng phần mười)
Lời giải:
a. Ta có: $12996=114\times 114$ nên độ dài cạnh miếng đất là $114$ (m)
b. $3,14 R^2=100$
$R^2=100:3,14$=31,84$
$R=\sqrt{31,84}=5,6$ (cm)
Đúng 1
Bình luận (0)
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
\(a)\sqrt {15} ;b)\sqrt {2,56} ;c)\sqrt {17256} ;d)\sqrt {793881} \)
Độ chính xác 0,005 tức là ta cần làm tròn đến hàng phần trăm
\(a)\sqrt {15}=3,8729...\approx 3,87\\b)\sqrt {2,56} = 1,6\\c)\sqrt {17256} =131,3620... \approx 131,36\\d)\sqrt {793881} = 891\)
Đúng 0
Bình luận (0)
Ta có thể áp dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí. Việc ước lượng này lại càng cần thiết khi sử dụng máy tính bỏ túi trong trường hợp xuất hiện những kết quả sai do ta bấm nhầm nút. Chẳng hạn, để ước lượng kết quả của phép nhân 6439. 384, ta làm như sau: - Làm tròn số đến chữ số ở hàng cao nhất mỗi thừa số: 6439≈6000; 384 ≈ 400. - Nhân hai số đã được làm tròn: 6000 . 400 2 400 000 Như vậy, tích phải tìm...
Đọc tiếp
Ta có thể áp dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí. Việc ước lượng này lại càng cần thiết khi sử dụng máy tính bỏ túi trong trường hợp xuất hiện những kết quả sai do ta bấm nhầm nút.
Chẳng hạn, để ước lượng kết quả của phép nhân 6439. 384, ta làm như sau:
- Làm tròn số đến chữ số ở hàng cao nhất mỗi thừa số:
6439≈6000; 384 ≈ 400.
- Nhân hai số đã được làm tròn:
6000 . 400 = 2 400 000
Như vậy, tích phải tìm sẽ là một số xấp xỉ 2 triệu.
Ở đây, tích đúng là: 6439 . 384 = 2 472 576
Theo cách trên, hãy ước lượng kết quả các phép tính sau
a) 495.52 ; b) 82,36.5,1 ; c) 6730 : 48
495 . 52 ≈ 500 . 50 = 25000.
⇒ Tích phải tìm có 5 chữ số xấp xỉ 25000.
82,36 . 5,1 ≈ 80. 5 = 400.
⇒ Tích phải tìm có 3 chữ số xấp xỉ 400.
6730 : 48 ≈ 7000 : 50 = 140.
⇒ Thương phải tìm xấp xỉ 140.
Đúng 0
Bình luận (0)
Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm :
(các kết quả tính góc được làm tròn đến phút và các kết quả tính độ dài và tính các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ tư)
\(\sin39^013';\cos52^018';tg13^020';cotg10^017';\sin54^0;\cos45^0\)
\(\sin39^013'=0,6322\)
\(\cos52^018'=0,6115\)
\(\tan13^020'=0,2370\)
\(\cot10^017'=5,5118\)
\(\sin54^0=0,8090\)
\(\cos45^0=0,7071\)
Đúng 0
Bình luận (0)
A) Hà sử dụng máy tính cầm tay để tính tổng của các số 22,5 ; 0,678 ; 138,4 và 23,1. Hà ước lượng kết quả tính là 184 nhưng máy tính lạ hiển thị kết quả là 60,118. Hãy cho biết trong khi Hà tính đã nhấn sai vị trí phím chỉ dấu phẩy của số thập phân nào trong các số thập phân nói trên ?B)Ngọc và 3 bạn khác sử dụng máy tính cầm tay để tính 5,24 + 23,87 - 2,092. Họ so sánh thì thấy kết quả có được của 4 người là : 5,535 ;26,19 ; 27,018 và 74,178. Hãy xác định câu trả lời đúng và chỉ ra từng lỗi sai...
Đọc tiếp
A) Hà sử dụng máy tính cầm tay để tính tổng của các số 22,5 ; 0,678 ; 138,4 và 23,1. Hà ước lượng kết quả tính là 184 nhưng máy tính lạ hiển thị kết quả là 60,118. Hãy cho biết trong khi Hà tính đã nhấn sai vị trí phím chỉ dấu phẩy của số thập phân nào trong các số thập phân nói trên ?
B)Ngọc và 3 bạn khác sử dụng máy tính cầm tay để tính 5,24 + 23,87 - 2,092. Họ so sánh thì thấy kết quả có được của 4 người là : 5,535 ;26,19 ; 27,018 và 74,178. Hãy xác định câu trả lời đúng và chỉ ra từng lỗi sai trong khi sử dụng máy tính với các câu trả lời còn lại ?
Sử dụng máy tính cầm tay làm tròn các số sau đến chữ số thập phân thứ nhất:
\(a = \sqrt 2 ;b = \sqrt 5 \)
Tính tổng hai số thập phân nhận được.
Ta có: a = 1,414…; b = 2,236
Làm tròn đến chữ số thập phân thứ nhất, ta được: \(a \approx 1,4;b \approx 2,2\)
Tổng 2 số thập phân nhận được là: 1,4 + 2,2 = 3,6
Đúng 0
Bình luận (0)