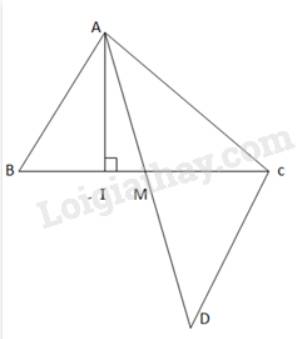
a)

AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}\) (đường vuông góc nhỏ hơn đường xiên)

b)

Lấy D sao cho M là trung điểm của AD

Xét \(\Delta ABM\) và \(DCM\) có

AM = DM ( do M là trung điểm của AD)

BM = CM ( do M là trung điểm của BC)

\(\widehat {AMB} = \widehat {CMD}\)( 2 góc đối đỉnh)

\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)

\( \Rightarrow AB = CD\)(2 cạnh tương ứng)

Xét  \(\Delta ADC\) ta có: AD < AC + CD (bất đẳng thức tam giác)

\( \Rightarrow \)   2AM < AC + AB

\( \Rightarrow \)   AM < \(\dfrac{1}{2}\)(AB + AC) 

Lấy D sao cho M là trung điểm của AD

Xét tứ giác ABDC có

M là trung điểm của AD

M là trung điểm của BC

Do đó: ABDC là hình bình hành

Suy ra: AB=DC
Xét ΔCAD có CA+CD>AD

=>CA+AB>2AM

hay AM<1/2(AB+AC)

Lời giải:

Bạn tự vẽ hình nhé.

a) Ta thấy \(\widehat{MFC}=90^0-\widehat{MAF}(1)\)

VÌ $AM$ là trung tuyến ứng với cạnh huyền nên \(AM=\frac{BC}{2}=BM=MC\)

\(\Rightarrow \triangle AMB\) cân tại $M$

\(\Rightarrow \widehat{MBE}=\widehat{MBA}=\widehat{MAB}=90^0-\widehat{MAF}(2)\)

Từ \((1);(2)\Rightarrow \widehat{MFC}=\widehat{MBE}\)

Xét tam giác $MBE$ và $MFC$ có:

\(\left\{\begin{matrix} \widehat{MBE}=\widehat{MFC}\\ \widehat{BME}=\widehat{FMC}(\text{đối đỉnh})\end{matrix}\right.\) \(\Rightarrow \triangle MBE\sim \triangle MFC(g.g)\)

b) Theo phần a thì \(\widehat{MBE}=\widehat{MFC}\Leftrightarrow \widehat{ABC}=\widehat{AFE}\)

Xét tam giác $ABC$ và $AFE$ có:

\(\left\{\begin{matrix} \widehat{ABC}=\widehat{AFE}\\ \text{chung góc A}\end{matrix}\right.\Rightarrow \triangle ABC\sim \triangle AFE(g.g)\)

\(\Rightarrow \frac{AB}{AF}=\frac{AC}{AE}\Rightarrow AB.AE=AC.AF\)

c)

Do $AH,AM$ là hai đường cao tương ứng đỉnh $A$ của hai tam giác đồng dạng $ABC$ và $AFE$ nên \(\frac{AH}{AM}=\frac{AB}{AF}=\frac{AC}{AE}\)

Do đó \(\frac{S_{ABC}}{S_{AEF}}=\frac{\frac{AB.AC}{2}}{\frac{AE.AF}{2}}=\frac{AB}{AF}.\frac{AC}{AE}=\left(\frac{AH}{AM}\right)^2(*)\)

Xét tam giác $AMI$ và $AHM$ có:

\(\left\{\begin{matrix} \text{chung góc A}\\ \widehat{AMI}=\widehat{AHM}=90^0\end{matrix}\right.\Rightarrow \triangle AMI\sim \triangle AHM(g.g)\)

\(\Rightarrow \frac{AM}{AI}=\frac{AH}{AM}(**)\)

Từ \((*);(**)\Rightarrow \frac{S_{ABC}}{S_{AEF}}=\left(\frac{AM}{AI}\right)^2\) (đpcm)

Xét tam giác ACM và tam giác ABM

CM=MB

góc B= goc C

AC=AB

SUY RA 2 TAM GIÁ BẰNG NHAU( c-g-c)

suy ra góc CAM= góc BAM

suy ra AM là tia phân giác

Bài 3: 

a) Xét ΔAMC và ΔDMB có 

MA=MD(gt)

\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)

MC=MB(gt)

Do đó: ΔAMC=ΔDMB(c-g-c)

Suy ra: \(\widehat{ACM}=\widehat{DBM}\)(hai góc tương ứng)

mà hai góc này là hai góc ở vị trí so le trong

nên AC//DB(Dấu hiệu nhận biết hai đường thẳng song song)

mà AC\(\perp\)AB(gt)

nên DB\(\perp\)AB

hay \(\widehat{ABD}=90^0\)

b) Xét ΔABD vuông tại B và ΔBAC vuông tại A có 

BA chung

BD=AC(ΔDMB=ΔAMC)

Do đó: ΔABD=ΔBAC(hai cạnh góc vuông)

c) Ta có: ΔABD=ΔBAC(cmt)

nên AD=BC(hai cạnh tương ứng)

mà \(AM=\dfrac{1}{2}AD\)(gt)

nên \(AM=\dfrac{1}{2}BC\)

Xét ΔABC có 

BD,CE là trung tuyến

BD cắt CE tại G

=>G là trọng tâm

=>M là trung điểm của BC

Lấy D sao cho M là trung điểm của AD

Xet tứ giác ABDC có

M là trung điểm chung của AD và BC

=>ABDC là hình bình hành

=>AD>AC+CD=AC+AB

=>AM<1/2(AB+AC)

bài 2:

ta có : điểm M nằm trên đường trung trực của BC nên M sẽ cách đều B và C => MB=MC

Ta có: AC=AM+MC

=> AC=AM+MB

Bài 2: Tam giác BNC cân tại N vì đường thẳng hạ từ N xuống vuong góc cạnh đối diện cũng là trung tuyến nên BN=NC

=> AN+BN=AN+NC=AC