Trong không gian Oxyz, một thiết bị phát sóng đặt tại vị trí A(2; 0; 0). Vùng phủ sóng của thiết bị có bán kính bằng 1.Hỏi vị trí M(2; 1; 1) có thuộc vùng phủ sóng của thiết bị nói trên hay không?

Những câu hỏi liên quan
Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại ba vị trí O(0;0), A(1; 0), B(1; 3) nhận được cùng một thời điểm. Hãy xác định vị trí phát tín hiệu âm thanh.
Gọi J là vị trí âm thanh phát đi. Ta có J cách đều O, A, B. Do đó J là giao của hài đường trun trực \({d_1},{d_2}\) tương ứng của OA, OB. Đường thẳng \({d_1}\) đi qua trung điểm M của OA và vuông góc với OA. Ta có \(M\left( {\frac{1}{2};0} \right)\) và \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {OA} = \left( {1;0} \right)\).
Phương trình đường thẳng \({d_1}\) là \(1\left( {x - \frac{1}{2}} \right) + 0\left( {y - 0} \right) = 0 \Leftrightarrow x = \frac{1}{2}\).
Tương tự, phương trình đường thẳng \({d_2}\) là \(x + 3y - 5 = 0\).
Tọa độ điểm J là nghiệm của hệ \(\left\{ \begin{array}{l}x = \frac{1}{2}\\x + 3y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{3}{2}\end{array} \right.\).
Vậy \(J\left( {\frac{1}{2};\frac{3}{2}} \right)\).
Đúng 0
Bình luận (0)
Cường độ của một sóng sẽ bị suy giảm khi truyền đi trong không gian. Khi sóng lan truyền, biên độ sóng giảm dần. Biết rằng cường độ sóng tỉ lệ với bình phương của biên độ sóng. Tại vị trí mà biên độ sóng giảm còn một nửa so với nguồn phát thì cường độ sóng tại đó thay đổi như thế nào so với tại nguồn?
Cường độ sóng I tỉ lệ với bình phương của biên độ sóng A.
\(I = k{A^2}\)(với k là hằng số).
Tại vị trí mà biên độ sóng giảm còn một nửa, cường độ sóng là \(I' = k{\left( {\frac{A}{2}} \right)^2} = \frac{1}{4}k{A^2} = \frac{I}{4}\).
Vậy cường độ sóng giảm đi 4 lần tại vị trí mà biên độ sóng giảm còn một nửa.
Đúng 0
Bình luận (0)
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/s2 cho biết khi dừng lại tại N (cổng nhà máy). Biết NO 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm là đẳng hướng và không hấp thụ âm....
Đọc tiếp
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/s2 cho biết khi dừng lại tại N (cổng nhà máy). Biết NO = 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm là đẳng hướng và không hấp thụ âm. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất
A. 20 s.
B. 25 s.
C. 15 s.
D. 10 s.
Đáp án D
+ Ta có:
L N - L M = 20 log ( OM ON ) ⇒ OM = 10 ON
Vậy MN = 135 m
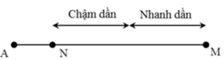
Xe chuyển động thành hai giai đoạn trên MN, nửa giai đoạn đầu là nhanh dần đều, nửa giai đoạn sau là chậm dần đều
→ t = 2 MN 2 a = 2 135 2 . 3 , 75 = 8 , 48 s .
Đúng 0
Bình luận (0)
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/
s
2
cho biết khi dừng lại tại N (cổng nhà máy). Biết NO 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường...
Đọc tiếp
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/ s 2 cho biết khi dừng lại tại N (cổng nhà máy). Biết NO = 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm là đẳng hướng và không hấp thụ âm. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất
A. 20 s.
B. 25 s.
C. 15 s.
D. 10 s.
Đáp án D
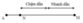
+ Ta có : L N - L M = 20 log O M O N ⇒ O M = 10 O N
Vậy MN=135m
Xe chuyển động thành hai giai đoạn trên MN, nửa giai đoạn đầu là nhanh dần đều, nửa giai đoạn sau là chậm dần đều
→ t = 2 M N 2 a = 2 135 2 . 3 , 75 = 8 , 48 s
Đúng 0
Bình luận (0)
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/s2 cho biết khi dừng lại tại N (cổng nhà máy). Biết NO 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm là đẳng hướng và không hấp thụ âm....
Đọc tiếp
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/s2 cho biết khi dừng lại tại N (cổng nhà máy). Biết NO = 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm là đẳng hướng và không hấp thụ âm. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất
A. 20 s.
B. 25 s.
C. 15 s.
D. 10 s.
Đáp án D

+ Ta có :
L N - L M = 20 log O M O N ⇒ O M = 10 O N
Vậy MN=135cm
Xe chuyển động thành hai giai đoạn trên MN, nửa giai đoạn đầu là nhanh dần đều, nửa giai đoạn sau là chậm dần đều
→ t = 2 M N 2 a = 2 135 2 . 3 , 75 = 8 , 48 s
Đúng 0
Bình luận (0)
Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm. Mức cường độ âm tại M là 70 dB, tại N là 30dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại trung điểm MN khi đó là A. 33,4 dB B. 36,1 dB C. 42,1 dB D. 41,2 dB
Đọc tiếp
Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm. Mức cường độ âm tại M là 70 dB, tại N là 30dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại trung điểm MN khi đó là
A. 33,4 dB
B. 36,1 dB
C. 42,1 dB
D. 41,2 dB
Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm thì mức cường độ âm tại M là 70dB, tại N là 50dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại N khi đó là A. 61,215dB B. 50,915dB C. 51,215dB D. 60,915dB
Đọc tiếp
Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm thì mức cường độ âm tại M là 70dB, tại N là 50dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại N khi đó là
A. 61,215dB
B. 50,915dB
C. 51,215dB
D. 60,915dB
Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm thì mức cường độ âm tại M là 70dB, tại N là 50dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại N khi đó là A. 61,215dB B. 50,915dB C. 51,215dB D. 60,915dB
Đọc tiếp
Ba điểm O, M, N cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng ra không gian, môi trường không hấp thụ âm thì mức cường độ âm tại M là 70dB, tại N là 50dB. Nếu chuyển nguồn âm đó sang vị trí M thì mức cường độ âm tại N khi đó là
A. 61,215dB
B. 50,915dB
C. 51,215dB
D. 60,915dB
Đáp án B
+ Ta có 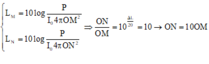 , chuẩn hóa OM=1
→
M
N
=
9
, chuẩn hóa OM=1
→
M
N
=
9
+ Mức cường độ âm tại N khi đặt nguồn tại M: ![]()
Đúng 0
Bình luận (0)
Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ kín đến bán kính 100 km.Người ta đặt một trạm phát sóng 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 20 km (Hình 23). Sóng 4G của trạm phát sóng A có thể phủ đến đảo đó được không? Vì sao?
Đọc tiếp
Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ kín đến bán kính 100 km.
Người ta đặt một trạm phát sóng 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 20 km (Hình 23). Sóng 4G của trạm phát sóng A có thể phủ đến đảo đó được không? Vì sao?
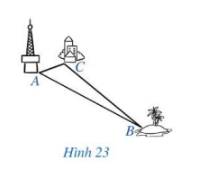
Ta xét tam giác ABC: \(AC = 20\) km, \(BC = 75\) km.
Và \(AC + BC = 20 + 75 = 95\) km. Mà tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại.
Hay \(AC + BC = 95\) > AB.
Do đó, AB < 100.
Vậy sóng 4G của trạm phát sóng A có thể phủ đến đảo B. (Vì sóng 4G có thể phủ kín đến bán kính 100 km).
Đúng 0
Bình luận (0)
tại vị trí O trong một nhà máy, một còi báo cháy ( xem là nguồn điểm ) phát âm với công suất không đổi. từ bên ngoài một thiết bị xác định mức cường âm chuyển động thẳng từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 0,4m/s^2 cho đến khi dừng lại tại N ( cổng nhà máy ) biết NO 10m và mức cường độ âm ( do còi phát ra ) tại N lớn hơn mức cường độ am tại M là 20dB. cho rằng môi trường truyền âm đẳng hướng và không hấp thụ âm. thời gian thiết bị đó chuyển độ...
Đọc tiếp
tại vị trí O trong một nhà máy, một còi báo cháy ( xem là nguồn điểm ) phát âm với công suất không đổi. từ bên ngoài một thiết bị xác định mức cường âm chuyển động thẳng từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 0,4m/s^2 cho đến khi dừng lại tại N ( cổng nhà máy ) biết NO = 10m và mức cường độ âm ( do còi phát ra ) tại N lớn hơn mức cường độ am tại M là 20dB. cho rằng môi trường truyền âm đẳng hướng và không hấp thụ âm. thời gian thiết bị đó chuyển động từ M đến N có giá trị là:
Câu hỏi này bạn cần biết phân tích chuyển động biến đổi đều của xe, quãng đường xe chuyển động và âm chuyển động để giải bài toán.
+ Biết mức cường độ âm tại N lớn hơn mức cường độ âm tại M là 20 dB, ta có:
\({{L}_{N}}-{{L}_{M}}=10.\lg{{\left( \dfrac{{{R}_{M}}}{{{R}_{N}}} \right)}^{2}}=20\Rightarrow {{R}_{M}}=OM=10{{R}_{N}}=100m\)
\(\Rightarrow MN = OM – ON = 90 m\)
Vật (thiết bị) đi từ M nhanh dần đều đến trung điểm của MN, sau đó chuyển động chậm dần và dừng lại tại N, nên ta có: \({{t}_{MN}}=2.{{t}_{MC}}\)(C là trung điểm của MN)
\(MC=\dfrac{MN}{2}=\dfrac{1}{2}at_{MC}^{2}\Rightarrow {{t}_{MC}}=\sqrt{\dfrac{MN}{a}}\)
\(\Rightarrow t={{t}_{MN}}=2\sqrt{\dfrac{MN}{a}}=2\sqrt{\dfrac{90}{04}}=30s\)
Vậy giá trị gần nhất là 32s
Đúng 0
Bình luận (0)











