Cho hbh ABCD kẻ AH và CK vuông với BD. gọi O là giao của AC và BD. CM H,O,K thẳng hàng

Những câu hỏi liên quan
Cho Hcn ABCD, O là giao điểm của AC và BD, M là trung điểm của AB, N là điểm đối xứng với O qua M.
a) Cm: Tứ giác ANBO là hình thoi.
b) Tính OM và diện tích h.thoi ANBO biết AB=12cm, BC=9cm
c) Kẻ AH vuông góc với BD (H thuộc BD), CK vuông góc với BD(K thuộc BD). Cm: tứ giác AHCK là h.b.hành.
d) Gọi F là giao điểm của DN và AC. Cm: CF=3/4 BD.
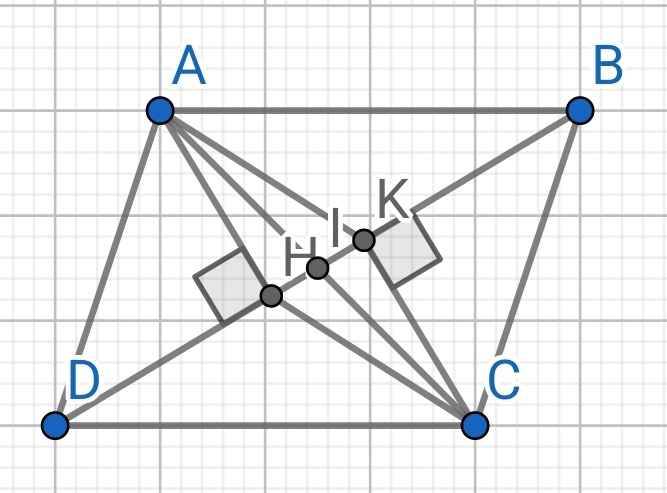
Cho hbh ABCD, kẻ AH vuông góc BD tại H,CK vuông góc BD tại K. a) CM: tứ giác giác AHCK là hbh b) Gọi I là trung điểm của HK.CM:IB=ID
 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ ∠ADH = ∠CBK (so le trong)
Do AH ⊥ BD (gt)
CK ⊥ BD (gt)
⇒ AH // CK
∆AHD và ∆CKB có:
AD = BC (hai cạnh đối của hình bình hành)
∠ADH = ∠CBK (cmt)
⇒ ∆AHD = ∆CKB (cạnh huyền - góc nhọn)
⇒ AH = CK (hai cạnh tương ứng)
Tứ giác AHCK có:
AH // CK (cmt)
AH = CK (hai cạnh tương ứng)
⇒ AHCK là hình bình hành
b) Do AHCK là hình bình hành (cmt)
I là trung điểm HK (gt)
⇒ I là trung điểm AC
Do ABCD là hình bình hành (gt)
I là trung điểm AC (cmt)
⇒ I là trung điểm BD
⇒ IB = ID
Đúng 6
Bình luận (0)
Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H và ở K.
a) chứng minh tứ giác AHCK là hình bình hành
b) gọi O là trung điểm của HK
c/m 3 điểm A,O,C thẳng hàng
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hbh
=>AC cắt HK tại trung điểm của mỗi đường
=>A,O,C thẳng hàng
Đúng 1
Bình luận (0)
cho tam giác ACD(AD<AC). Gọi O là trung điểm AC, Trên đường thẳng DO lấy điểm B sao cho DO=OB
a). Chứng minh tứ giác ABCD là hình bình hành
b). Kẻ AH và CK lần lượt vuông góc với BD tại H và K. Chứng minh O là trung điểm HK
a: Xét tứ giác ABCD có
O là trung điểm chung của AC và BD
=>ABCD là hình bình hành
b: Xét ΔOHA vuông tại H và ΔOKC vuông tại K có
OA=OC
\(\widehat{AOH}=\widehat{COK}\)
Do đó: ΔOHA=ΔOKC
=>OH=OK
=>O là trung điểm của HK
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, Kẻ AH; Ck vuông góc với đường chéo BD:
a) CM AHCK là hình bình hành
b) Gọi O là giao điểm của AC và BD. CHứng tỏ H,O,K thẳng hàng.
a) Xét hai tam giác vuông ADH và BCK có:
AD = BC (tính chất hình bình hành)
\(\widehat{B_1}=\widehat{D_2}\) (slt, AB // CD)
Vậy: \(\Delta ADH=\Delta BCK\left(ch-gn\right)\)
\(\Rightarrow\) AH = CK (1)
Chứng minh tương tự ta được: \(\Delta ABK=\Delta CDH\left(ch-gn\right)\)
\(\Rightarrow\) AK = CH (2)
Từ (1) và (2) suy ra: AHCK là hình bình hành
b) O là giao điểm của AC và BD thì O là trung điểm của AC (tính chất đường chéo hình bình hành)
AHCK là hình bình hành (cmt) \(\Rightarrow\) HK đi qua trung điểm O của đường chéo AC
Vậy H, O, K thẳng hàng.
Đúng 0
Bình luận (1)
Cho HCN ABCD, AB=8cm, BC=6cm. Gọi H là hình chiếu của A trên BD. O là giao điểm 2 đường chéo AC và BD. Qua O kẻ đuồng thẳng song song với AH cắt AD tại E và cắt AB tại I . Cm: IA.BE=IB.AE
Cho hình thang cân ABCD ( AB//CD , AB < DC ) . Kẻ AH vuông góc vs AB cắt DB tại h . Kẻ BK vuông góc với AB và cắt AC tại K a) Tứ giác AHKB là hình gì . tại sao b) gọi E là trung điểm cua AB , F là trung điểm của DC . gọi i là giao diểm của AC và BD , g là giao điểm của ch và dk . cm : ei , g , f thẳng hàng
1) Tam giác vuông ABH = tam giác vuông BAK (Góc vuông A = góc vuông B, cạnh AB chung, góc \(\widehat{KAB}=\widehat{HBA}\))
=> AH = BK
Mà AH // BK cì cùng vuông góc với AB => ABKH là hình bình hành, lại có 2 góc vuông nên nó là hình chữ nhật
b) Gọi O là trung điểm của HK. Ta có E, I , O thẳng hàng do ABKH là hình chữ nhật (các bạn tự chứng minh)
HK // AB // DC => E, O, F thẳng hàng
HKDC là hình thang cân => O, G, F cũng thẳng hàng
=> E, I, O, G, F thảng hàng
Đúng 1
Bình luận (1)
Cho đường tròn (O;R), và các tiếp tuyến AB,AC căt nhau tại A nằm ngoài đường tròn(B,C là các tiếp điểm).Gọi H là giao điểm của BC và OA
a)CM: OAvuông góc với BC và OH.OA=R^2
b)Kẻ đường kính BD của đường tròn (O) và đường thẳng CD vuông góc với BD (K thuộc BD).CM OA song song với CD và AC.CD=CK.AO
c)Gọi I là giao điểm của AD và CK. CM:tam giác BIK và tam giác CHK có diện tích bằng nhau.
a, Vì OB = OC ( =R )
AB = AC (tiếp tuyến)
=> OA là trung trực BC
=> OA vuông góc BC
Vì AB là tiếp tuyến (O)
\(\Rightarrow OB\perp AB\)
=> t/g OAB vuông tại B
Xét t/g OAB vuông tại B có BH là đường cao
=>\(OH.OA=OB^2=R^2\)(hệ thức lượng)
b,* Xét \(\Delta\)BCD có : OB = OC = OD (=R)
=> \(\Delta\)BCD vuông tại C
=> \(BC\perp CD\)
Mà \(BC\perp OA\)
=> CD // OA
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Gọi O là giao điểm của 2 đg chéo AC và BD. Lấy điểm M trên cạnh CD và điểm N trên cạnh AB sao cho DM=BN
1) Chứng minh rằng:ANCM là hbh. Từ đó chứng minh 3 điểm M,O,N thẳng hàng
2) Tính diện tích hbh ANCM nếu AB = 4cm, AD = 3cm, BN= 1cm
3) Qua M kẻ MI song song vs AC (I thuộc AD), qua N kẻ NK song song vs AC (K thc BD). CM rằng IN // MK
















