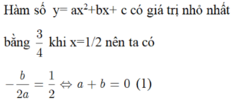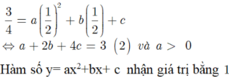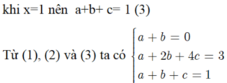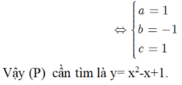Xác định hàm số y=ax2+bx+2 biết (P) đi qua B(-1;6) và có tung độ đỉnh là -1/4

Những câu hỏi liên quan
xác định hàm số bậc hai ax2+bx+c biết rằng đồ thị hàm số là parabol đi qua điểm B<0,4> và có đỉnh I <1,5>
Theo đề, ta có: c=4
Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\-\dfrac{b^2}{16a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2+80a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-20\\b=40\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 12. Xác định hàm số bậc hai y = ax2 + bx + c biết đồ thị của nó có đỉnh I(1; −1) và đi qua điểm A(2; 0)
A. y = x 2 − 3x + 2. B. y = 2x 2 − 4x + 3. C. y = x 2 − 2x. D. y = x 2 + 2x
Xác định parabol (P) ; y ax2+bx+ c biết: Hàm số y ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x1/2 và nhận giá trị bằng khi x1. A. y x2+ x+1. B. y- x2-x+1. C. y -x2-x-1. D. y x2-x+1
Đọc tiếp
Xác định parabol (P) ; y= ax2+bx+ c biết: Hàm số y= ax2+bx+ c có giá trị nhỏ nhất bằng 3/4 khi x=1/2 và nhận giá trị bằng khi x=1.
A. y= x2+ x+1.
B. y=- x2-x+1.
C. y= -x2-x-1.
D. y= x2-x+1
Xác định các hệ số a,b,c biết parabol y = ax2+bx+cax2+bx+c đi qua điểm A(2;3) và có đỉnh I ( 1;2 )
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua điểm B(-1; 6) và tung độ của đỉnh là -1/4.
+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
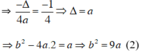
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.
Đúng 1
Bình luận (0)
Cho (P) : y=ax2+bx+c đi qua điểm F(0;5) và coa đỉnh I(3:-4)
a) xác định (P)
b) Khảo sát số biến thiên và vẽ đồ thị hàm số (P) vừa tìm được
a.
Do (P) đi qua F, thay tọa độ F vào phương trình (P) ta được:
\(a.0^2+b.0+c=5\Rightarrow c=5\)
Do (P) có đỉnh \(I\left(3;-4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=3\\a.3^2+b.3+c=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3b+5=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-6a\\9a+3.\left(-6a\right)=-9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-6\end{matrix}\right.\)
hay pt (P) có dạng: \(y=x^2-6x+5\)
b. Em tự giải
Đúng 1
Bình luận (0)
Xác định a, b, c biết parabol y = ax2 + bx + c Đi qua ba điểm A(0 ; -1), B(1 ; -1), C(-1 ; 1)
(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.
Đúng 0
Bình luận (0)
Xác định hệ số a của hàm y = a x 2 , biết rằng đồ thị của nó đi qua điểm A(-2; 1).Vẽ đồ thị của hàm số đó.
Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 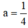
Vậy hàm số: 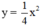
| x | -4 | -2 | 0 | 2 | 4 |
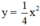 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
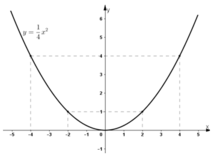
Đúng 0
Bình luận (0)
Xác định hệ số a của hàm y = a x 2 , biết rằng đồ thị của nó đi qua điểm A(-2; 1).Vẽ đồ thị của hàm số đó.
Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 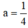
Vậy hàm số: 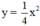
| x | -4 | -2 | 0 | 2 | 4 |
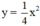 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
Đúng 0
Bình luận (0)
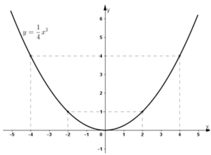
Bài 12: a)Xác định hệ số a của hàm số y = ax2, biết rằng đồ thị hàm số đi qua điểm A(2;-1)
b) Vẽ đồ thị của hàm số đó
CÓ AI CÒN THỨC KO VẬYY
Lời giải:
a) Vì ĐTHS đi qua điểm $A$ nên:
$y_A=ax_A^2$
$\Leftrightarrow -1=a.2^2\Rightarrow a=-\frac{1}{4}$
b) Vậy hàm số có công thức: $y=\frac{-1}{4}x^2$
Hình vẽ:
Đúng 1
Bình luận (0)