Cho ba điểm A(0; – 1; 1), B(1; 0; 5), G(1; 2; 0).
a) Chứng minh rằng ba điểm A, B, G không thẳng hàng.
b) Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.
Trong không gian Oxyz, cho ba điểm A(a;0;0),B(0,b,0) và C(0;0;c),(abc≠0) Viết phương trình mặt phẳng qua ba điểm A,B và C
A. A B C : x a - y b + z c = 1
B. A B C : x a + y b + z c = 1
C. A B C : x a + y b + z c = 0
D. A B C : x a + y b + z c + 1 = 0
Cho hai bộ ba điểm: A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1). Hỏi bộ nào có ba điểm thẳng hàng?
Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó 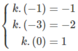
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a > 0, b > 0) và C(1; 2) như trên hình 12.
a) Viết phương trình đường thẳng đi qua hai điểm A, B.
b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.
c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.

Cho \(\text{A(0; 5), B(-3; 0), C(1; 1), M(-4,5; -2,5).}\)
a) CMR: ba điểm A, B, M thẳng hàng và ba điểm A, B, C không thẳng hàng.
b) Tính diện tích tam giác ABC.
Cho ba điểm A( 2;0), B ( 0; -2), C (3;1). Chứng tỏ rằng ba điểm A, B, C thẳng hàng.
Cho A(4; 0; 0), B(0; 2; 0), C(0; 0; 1) và D(2; 2; 0). Có bao nhiêu tam giác vuông có ba đỉnh là ba trong số 5 điểm O, A, B, C, D.
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.
Cho ba điểm A(0; 1), B(1; 2), C(-5; -4).
a)Viết phương trình đường thẳng d đi qua hai điểm A và B.
b) Chứng minh ba điểm A, B, C thẳng hàng.
Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
Cho ba điểm A(1; 1), B(4;3) và C(0;- 2).
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm toạ độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD= 2AB.
a) Ta có: \(\overrightarrow {AB} = \left( {3;2} \right),\overrightarrow {AC} = \left( { - 1; - 3} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Giả sử tọa độ điểm D là:\(D\left( {{x_D},{y_D}} \right)\)
Ta có: \(\overrightarrow {CD} = \left( {{x_D} - 0;{y_D} - \left( { - 2} \right)} \right) = \left( {{x_D};{y_D} + 2} \right)\)
Để tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Vậy nên \(\overrightarrow {CD} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2.3\\{y_D} + 2 = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 2\end{array} \right.\)
Vậy tọa độ D là: \(D\left( {6;2} \right)\)
Trong không gian cho ba điểm A, B, C.
Xác định điểm G sao cho: G A → + 2 G B → - 2 G C → = 0 →