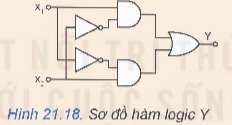
Cho hàm logic y = \(\overline{A}\) + BC hãy vẽ sơ đồ của hàm logic này sử dụng các cổng logic cơ bản đã học ở trên.
Những câu hỏi liên quan
Sử dụng tư duy logic của mình để tìm số còn thiếu trong sơ đồ dưới đây.
Đọc tiếp
Sử dụng tư duy logic của mình để tìm số còn thiếu trong sơ đồ dưới đây.
TL:
Vì 7 + 3 = 10 : 2 = 5 nên ta có thể suy luận ra:
Lấy 4 + 2 = 6 : 2 = 3
Đáp án: 3
HT
Xem thêm câu trả lời
Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 11:43
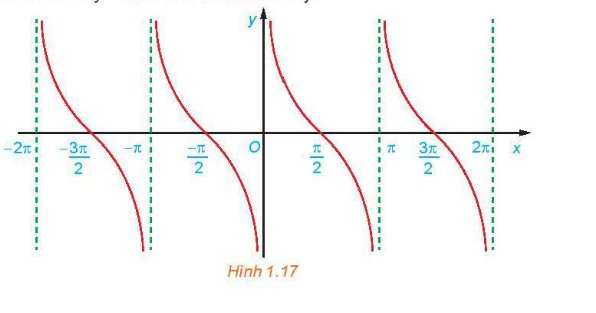
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−π2;2π] để hàm số y=cotx nhận giá trị dương.
cot x>0
=>\(x\in\left(0;\dfrac{pi}{2}\right)\cup\left(pi;\dfrac{3}{2}pi\right)\)
Đúng 0
Bình luận (0)
Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 11:37
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn [−\(\dfrac{\pi}{2}\);2π]
để hàm số y=cotx
nhận giá trị dương
Giải mục 1 trang 22, 23 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 9:22
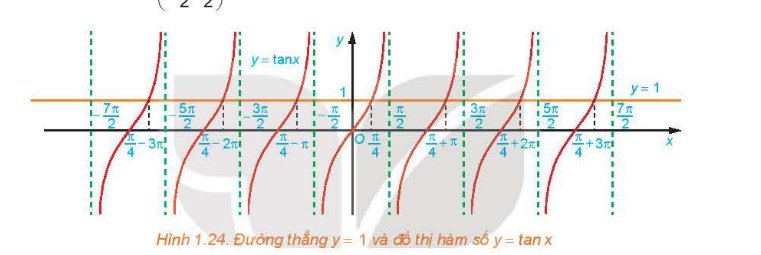
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn [−π;\(\dfrac{3\pi}{2}\)] để hàm số y=tanx
nhận giá trị âm.
tan x<0
=>\(x\in\left(-\dfrac{pi}{2};0\right)\cup\left(\dfrac{pi}{2};pi\right)\)
Đúng 0
Bình luận (0)
Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.
Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)
Đúng 0
Bình luận (0)
Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\) để hàm số \(y = \tan x\) nhận giá trị âm.
Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)
Đúng 0
Bình luận (0)
Lôgic toán là một ngành con của toán học có liên hệ gần gũi với cơ sở toán học, khoa học máy tính lý thuyết, logic triết học. Ngành này bao gồm cả hai phần: Nghiên cứu toán học về logic và những ứng dụng của logic hình thức trong các ngành khác của toán học. Các chủ đề thống nhất trong logic toán học bao gồm các nghiên cứu về sức mạnh ý nghĩa của các hệ thống hình thức và sức mạnh suy diễn của hệ thống chứng minh chính thức.Ngành này thường được chia thành các lĩnh vực con như lý thuyết mô hình...
Đọc tiếp
Lôgic toán là một ngành con của toán học có liên hệ gần gũi với cơ sở toán học, khoa học máy tính lý thuyết, logic triết học. Ngành này bao gồm cả hai phần: Nghiên cứu toán học về logic và những ứng dụng của logic hình thức trong các ngành khác của toán học. Các chủ đề thống nhất trong logic toán học bao gồm các nghiên cứu về sức mạnh ý nghĩa của các hệ thống hình thức và sức mạnh suy diễn của hệ thống chứng minh chính thức.
Ngành này thường được chia thành các lĩnh vực con như lý thuyết mô hình (model theory), lý thuyết chứng minh (proof theory), lý thuyết tập hợp và lý thuyết đệ quy (recursion theory). Nghiên cứu về lôgic toán thường đóng vai trò quan trọng trong ngành cơ sở toán học (foundations of mathematics).
Các tên gọi cũ của lôgic toán là lôgic ký hiệu (để đối lập với lôgic triết học) hay mêta toán học.
Lôgic toán không phải là lôgic của toán học mà là toán học của lôgic. Ngành này bao gồm những phần của lôgic mà có thể được mô hình hóa và nghiên cứu bằng toán học. Nó cũng bao gồm những lĩnh vực thuần túy toán học như lý thuyết mô hình và lý thuyết đệ quy, trong đó, khả năng định nghĩa là trung tâm của vấn đề được quan tâm.logic toán học thể hiện ở cách làm bài. Một bài toán được coi là lôgic thì phải đảm bảo sự chặt chẽ, cách lập luận hợp lý và tuân thủ theo từng bước của bài toán.
SGK Chân trời sáng tạo - Trang 88
25 tháng 7 2023 lúc 10:15
Em hãy sử dụng biểu thức logic viết các câu lệnh rẽ nhánh dạng thiếu hoặc dạng đủ để tính tiền vé xem phim cho các ngày thứ Năm, thứ Sáu, thứ Bảy và Chủ Nhật.
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học theo sơ đồ trên.
y = ax + b
y = a x 2 + b x + c
* Hàm số y = ax + b
Trường hợp a > 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = a > 0. Vậy hàm số đồng biến trên toàn bộ R.
QUẢNG CÁO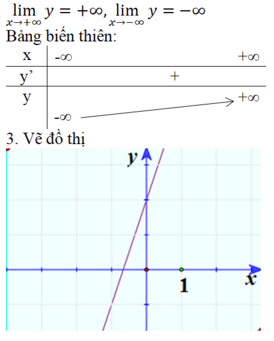
Trường hợp a < 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = a < 0. Vậy hàm số đồng biến trên toàn bộ R.
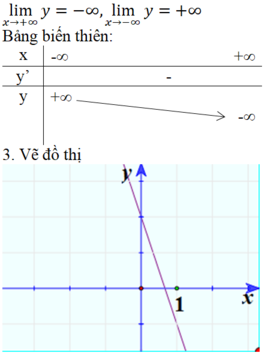
* Hàm số y = ax2 + bx + c
Trường hợp a > 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = 2ax + b. Cho y’ = 0 thì x = - b/2a.
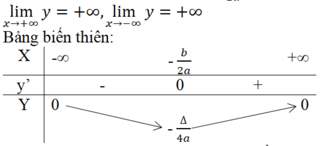
Hàm số nghịch biến trên khoảng (-∞,- b/2a).
Hàm số đồng biến trên khoảng [- b/2a, +∞].
Hàm số đạt cực tiểu bằng - Δ/4a tại x = - b/2a .
3. Vẽ đồ thị:
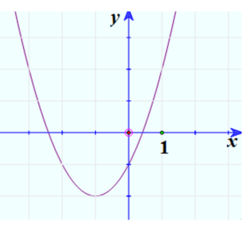
Trường hợp a < 0
1. TXĐ: D = R.
2. Sự biến thiên.
y’ = 2ax + b. Cho y’ = 0 thì x = - b/2a.
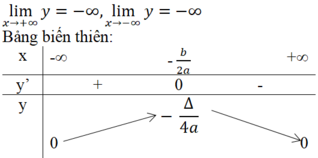
Hàm số đồng biến trên khoảng (-∞,- b/2a).
Hàm số nghịch biến trên khoảng [- b/2a, +∞].
Hàm số đạt cực đại bằng - Δ/4a tại x = - b/2a .
3. Vẽ đồ thị:
Đúng 0
Bình luận (0)
chữa lỗi diễn đạt (logic) của các câu saua, Từ này về dạy học ở trường này, các em học sinh làm cho tôi rất hài lòng.b, Nước giếng này trong mà lại gần nhà.c, Tôi bị hai vết thương,một ở chân, một ở quảng trị.d, Anh ta đóng cửa xe oto lại ngồi vào trước vô lăng rồi nổ máy phóng đi.e, Chàng dũng sĩ lao về phía con quái vật ,mồm ngoác to bằng cái miệng thúng.f, Dẫn bóng xuống tận cuối sân, Công Vinh vuốt bóng má ngoài chân trái , chi tọt vào lưới.g,Mới vào bộ đội, ngời cán bộ phổ biến: Chiến sĩ tr...
Đọc tiếp
chữa lỗi diễn đạt (logic) của các câu sau
a, Từ này về dạy học ở trường này, các em học sinh làm cho tôi rất hài lòng.
b, Nước giếng này trong mà lại gần nhà.
c, Tôi bị hai vết thương,một ở chân, một ở quảng trị.
d, Anh ta đóng cửa xe oto lại ngồi vào trước vô lăng rồi nổ máy phóng đi.
e, Chàng dũng sĩ lao về phía con quái vật ,mồm ngoác to bằng cái miệng thúng.
f, Dẫn bóng xuống tận cuối sân, Công Vinh vuốt bóng má ngoài chân trái , chi tọt vào lưới.
g,Mới vào bộ đội, ngời cán bộ phổ biến:" Chiến sĩ trai phải cắt tóc ngắn, chiến sĩ gái thì tết tóc lên cao, râu phải cạo ngắn.