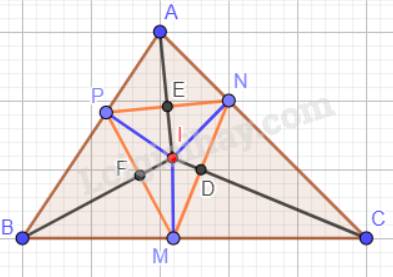
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.

Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.

Xét tam giác vuông INC và tam giác vuông IMC:

     IC chung;

     IN = IM.

Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).

Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).

     \(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).

Xét hai tam giác IDN và IDM có:

     ID chung;

     \(\widehat {NID} = \widehat {MID}\);

     IN = IM.

Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)

\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);

 \(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)

Mà  \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)

\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).

Suy ra: IC là đường trung trực của cạnh MN.

Tương tự ta có:

IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.

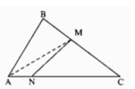
Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được

MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.

Trong tam giác ABC có AB ≤ AC, M ∈ BC (M ≠ B, M ≠ C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.

Gọi E là giao điểm các đường trung trực của MN và BC.

Theo tính chất đường trung trực ta có \(\left\{{}\begin{matrix}EM=EN\\EB=EC\end{matrix}\right.\).

Lại có BM = CN (gt) nên \(\Delta EMB=\Delta ENC(c.c.c)\).

Suy ra \(\widehat{EMB}=\widehat{ENC}\) nên \(\widehat{EMA}=\widehat{END}\).

Lại có BM = CN và AB = CD nên AM = ND.

Xét \(\Delta EMA\) và \(\Delta END\) có: \(\left\{{}\begin{matrix}AM=ND\\\widehat{EMA}=\widehat{END}\\EM=EN\end{matrix}\right.\)

\(\Rightarrow\Delta EMA=\Delta END\left(c.g.c\right)\Rightarrow EM=EN\).

Suy ra E thuộc đường trung trực của MN.

Vậy đường trung trực của ba đoạn AD, MN, BC đồng quy.

a, C/m CP // AB
Xét ΔANM và ΔCNP. Ta có:
NM = NP (gt)
∠N₁ = ∠N₂ (đối đỉnh)
NA = NC (gt)
⇒ ΔANM = ΔCNP (c.g.c)
Nên: ∠A = ∠C₁ (hai góc tương ứng)
Mà ∠A và ∠C₁ ở vị trí so le trong
⇒ CP // AB
b, C/m MB = CP
Ta có: MA = CP (vì ΔANM = ΔCNP)
Mà MA = MB (gt)
⇒ MB = CP
c, C/m BC = 2MN
Nối BP. Xét ΔMBP và ΔCPB. Ta có:
BM = CP (gt)
∠B₁ = ∠P₁ (so le trong)
BP cạnh chung
⇒ ΔMBP = ΔCPB (c.g.c)
Nên: MP = BC (hai cạnh tương ứng)
Mà: MP = 2MN (vì N là trung điểm của MP)
⇒ BC = 2MN
 

Xin lỗi,mk mới hok lớp 6 thui à!

Tham khảo:

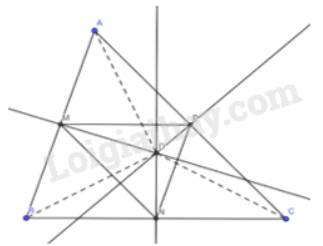
Theo giả thiết ta có :

OA = OB, MA = MB ( do M là trung điểm AB )

\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB

\( \Rightarrow \) MO vuông góc với AB

Theo giả thiết ta có :

OA = OC, PC = PA ( do P là trung điểm AC )

\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC

\( \Rightarrow \) PO vuông góc với AC

Theo giả thiết ta có :

OC = OB, NC = NB ( do N là trung điểm BC )

\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC

\( \Rightarrow \) NO vuông góc với BC