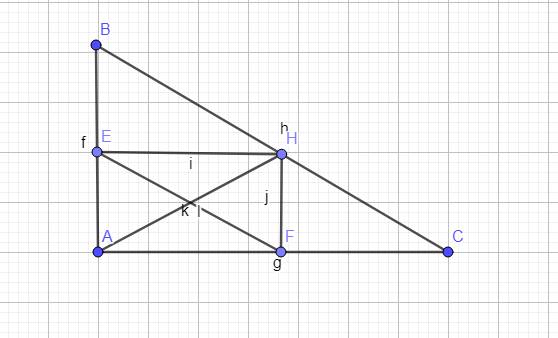
Cho tam giác ABC vuông tại A, đường cao AH. Hạ HE\(\perp\)AB, HF\(\perp\)AC. Chứng minh
a)\(\sqrt{S_{BEH}}\)+\(\sqrt{S_{CFH}}\)=\(\sqrt{S_{ABC}}\)
b)\(\frac{AH^2}{BE.CF}\)=\(\frac{AC}{AB}+\frac{AB}{AC}\)
c) Trong trường hợp AB<AC. Chứng minh sin2C=2sinC.cosC