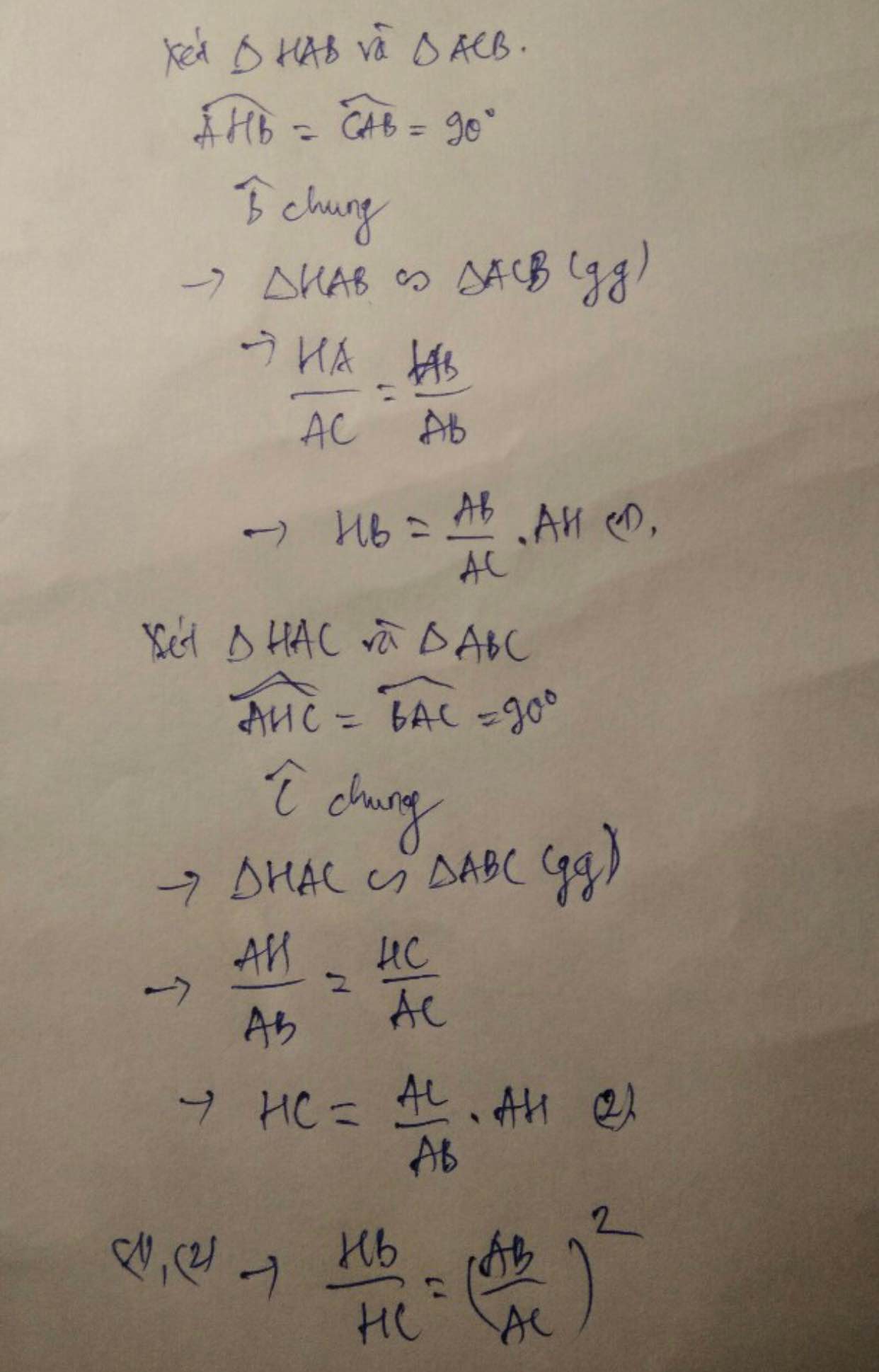cho ΔABc vuông tại A, kẻ đường trung tuyến AM và đường cao A. Gọi D,E lần lượt là hình chiếu của H trên AB,AC.
a) Chứng minh rằng DE2=BH.HC
b) Chứng minh DE vuông góc AM
Cho ∆ABC vuông tại A, đường cao AH. Biết HB=4cm, CH=9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.
a, Tính DE
b, Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N. Chứng minh MN=1/2BC
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Xét tứ giác ADHE có
\(\widehat{EAD}=90^0\)(gt)
\(\widehat{AEH}=90^0\)(gt)
\(\widehat{ADH}=90^0\)(gt)
Do đó: ADHE là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AH=DE(hai đường chéo của hình chữ nhật ADHE)
mà AH=6cm(cmt)
nên DE=6cm
Cho ΔABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh: AH = DE.
b) Chứng minh: ∠ADE = ∠BHD
c) Gọi M là trung điểm của BC. Chứng minh: DE = AM
a: Xét tứ giác AEHD có
\(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\)
Do đó: AEHD là hình chữ nhật
Suy ra: AH=DE
Cho ΔABC vuông tại A, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh: AH = DE.
b) Chứng minh: ∠ADE = ∠BHD
c) Gọi M là trung điểm của BC. Chứng minh: DE = AM
a, Vì \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\) nên ADHE là hcn
Do đó AH=DE
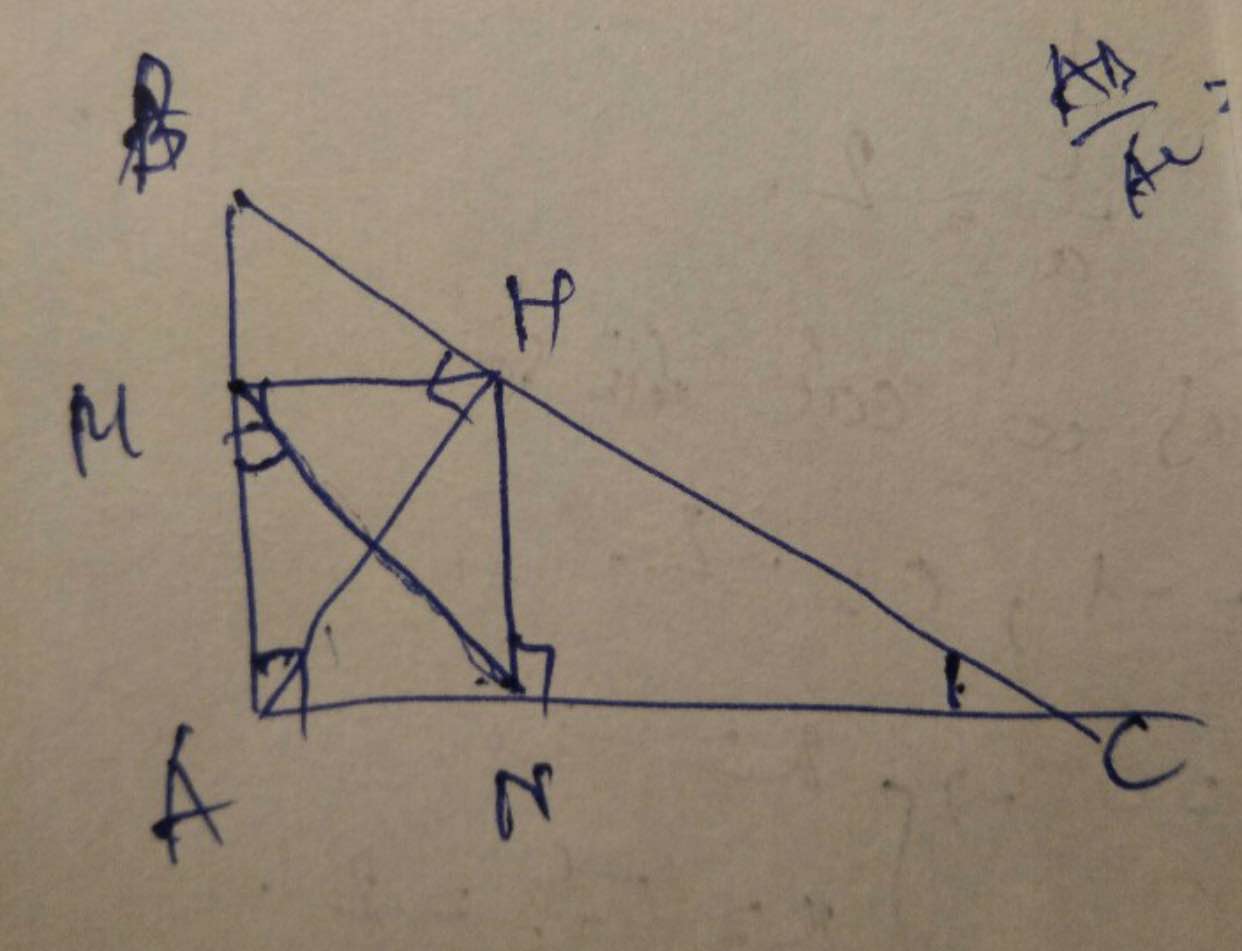
Cho tam giác ABC vuông tại A,đường cao AH.Gọi M,N lần lượt là hình chiếu của H trên AB,AC.Chứng minh HB/HC=(AB/AC)^2
Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến AM. Gọi D và E thứ tự là hình chiếu của H trên AB, AC.
a) Chứng minh rằng tam giác ABC đồng dạng tam giác HBA.
b) Cho HB = 4cm, HC = 9cm. Tính AB, DE.
c) Chứng minh AD.AB = AE.AC và AM vuông góc DE.
d) Tam giác ABC phải có điều kiện gì để diện tích tam giác ADE bằng 1/3 diện tích tứ giác BDEC.
Mọi người giúp em với ak""""
a, Xét \(\Delta ABC\left(\perp A\right)\) và \(\Delta HBA\left(\perp H\right)\) có \(\widehat{B}\) chung
b,\(\Delta ABC\sim\Delta HBA\) theo a
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\Leftrightarrow AB^2=HB.BC\)
\(=4.\left(4+9\right)\)
\(\Rightarrow AB=2\sqrt{13}\) (cm)
Áp dụng định lí py-ta-go trong \(\Delta ABH\):
\(AH=\sqrt{AB^2-BH^2}=6\left(cm\right)\)
Vì \(AH=DE=6cm\)
c, Xét \(\Delta HBA\left(\perp H\right)\) và \(\Delta DHA\left(\perp D\right)\) có \(\widehat{A}\) chung
\(\Rightarrow\Delta HBA\sim\Delta DHA\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AH}{AB}\Rightarrow AD.AB=AH^2\) \(\left(1\right)\)
Tương tự \(\Delta EHA\sim\Delta HCA\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AE.AC=AH^2\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow AD.AB=AE.AC\)
-Chúc bạn học tốt-
Cho tam giác ABC vuông tại A, đường cao AH.Gọi D, E lần lượt là hình chiếu của H trên AB , AC . Biết rằng BH=4, CH=9
a, Tính độ dài đoạn DE
b,CM AD.AB=AE.AC
cho tap hop A = { 1;2;3;4;.......;n} . Tìm số tự nhiên n biết tổng các phần tử của A bằng 90
cho tam giác ABC vuông tại A đường cao AH ,trung tuyến AM . Gọi D và E lần lượt là hình chiếu của H trên AB và AC.
a)chứng minh ADHE là hình chữ nhật.
b.chứng minh AM vuông góc DE
c.biết AB=6cm,AC=8cm.tính DE? d.Gọi N là giao điểm của AM và HE.K là hình chiếu của điểm M trên AB.CMR: MK,BN,AH đồng quy
mọi người giúp tớ với hic:<
a: Xét tứ giác ADHE có góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
=>DE=AH
=>\(DE^2=BH\cdot CH\)
b: Ta có: ΔABC vuông tại A
mà AM là trung tuyến
nên MA=MC
=>ΔMAC cân tại M
=>góc MAC=góc MCA
Vì ADHE là hình chữ nhật nên góc AED=góc AHD=góc ABC
=>góc AED+góc MAC=90 độ
=>AM vuông góc với DE
c: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(DE=AH=\dfrac{AB\cdot AC}{CB}=4.8\left(cm\right)\)
cho tam giác ABC vuông tại A có đường cao AH.Gọi M,N lần lượt là hình chiếu của H lên AB,AC.
a)chứng minh HMAN là hình chữ nhật
b)Gọi O là giao điểm cũa AH và MN.I,K là trung điểm của BH và HC.CHứng minh BO vuông góc với AK
c)Chứng minh:MIKN là hình thang vuông
cho tam giác ABC vuông tại A có đường cao AH.Gọi M,N lần lượt là hình chiếu của H lên AB,AC.
a)chứng minh HMAN là hình chữ nhật
b)Gọi O là giao điểm cũa AH và MN.I,K là trung điểm của BH và HC.CHứng minh BO vuông góc với AK
c)Chứng minh:MIKN là hình thang vuông
