`x^2 -4x+4-y^2`

`=(x^2 -4x+4)-y^2`

`=(x-2)^2 -y^2`

`=(x-2-y)(x-2+y)`

`x^2+2xy+y^2-x-y`

`=(x^2+2xy+y^2) -(x+y)`

`=(x+y)^2 -(x+y)`

`=(x+y)(x+y-1)`

`x^2-2xy+y^2-9`

`=(x^2-2xy+y^2)-3^2`

`=(x-y)^2-3^3`

`=(x-y-3)(x-y+3)`

Tách ra đi cậu.

x²+y²-4x+6y+13=0

(x²-4x+4)+(y²+6y+9)=0

(x-2)²+(y+3)²=0

suy ra x-2=0 hoặc y+3=0

*x-2=0=>x=2      *y+3 =0=> y=-3

vậy x=2,y=-3

Đáp án A

Ta có, giả thiết  log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính  R 1 = 2

Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m  là đường tròn tâm I(-2;-3); R 2 = m  

Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9

\(C=x^2+y^2+4x-6y+1\)

\(=x^2+4x+4+y^2-6y+9-12\)

\(=\left(x+2\right)^2+\left(y-3\right)^2+1\)

\(=30^2+10^2+1\)

=1001

a: \(x^2+3y^2-4x+6y+7=0\)

\(\Leftrightarrow x^2-4x+4+3y^2+6y+3=0\)

\(\Leftrightarrow\left(x-2\right)^2+3\left(y+1\right)^2=0\)

\(\Leftrightarrow\left(x,y\right)=\left(-2;1\right)\)

Đáp án A

Ta có, giả thiết

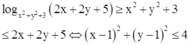
là miền trong đường tròn tâm I(1;1) bán kính R₁ = 2

Và 

Cách 1 : Xác định các hệ số a, b, c.

a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2

⇒ tâm I (1; 1) và bán kính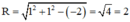 

b) 16x2 + 16y2 + 16x – 8y –11 = 0

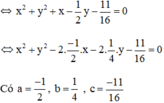
⇒ Đường tròn có tâm 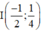 , bán kính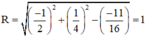 

c) x2 + y2 - 4x + 6y - 3 = 0

⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0

có hệ số a = 2, b = -3,c = -3

⇒ Đường tròn có tâm I(2 ; –3), bán kính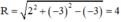 

Cách 2 : Đưa về phương trình chính tắc :

a) x2 + y2 - 2x - 2y - 2 = 0

⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4

⇔(x-1)2 + (y-1)2 = 4

Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.

b) 16x2 + 16y2 + 16x - 8y - 11 = 0

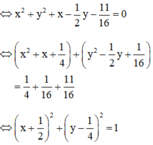
Vậy đường tròn có tâm 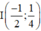 và bán kính R = 1.

c) x2 + y2 - 4x + 6y -3 = 0

⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3

⇔ (x - 2)2 + (y + 3)2 = 16

Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.

Đáp án D

\(x^2-4x+y^2-6y+15=2\)

\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2-9y+9\right)+2=2\)

\(\Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2=0\)

Vì \(\left(x-2\right)^2\ge0;\left(y-3\right)^2\ge0\) 

Mà \(\left(x-2\right)^2+\left(y-3\right)^2=0\)

\(\Rightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=0\\\left(y-3\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)

Vậy (x;y) = (2;3)

\(\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)

\(\Leftrightarrow\left(x-2\right)^2+\left(y-3\right)^2=0\)

Do \(\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\\\left(y-3\right)^2\ge0\end{matrix}\right.\) ;\(\forall x;y\Rightarrow\left(x-2\right)^2+\left(y-3\right)^2\ge0\)

Đẳng thức xảy ra khi và chỉ khi:

\(\left\{{}\begin{matrix}x-2=0\\y-3=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)