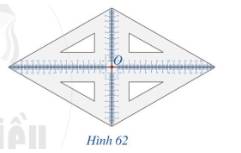
Lấy bốn chiếc ê ke giống nhau để xếp thành hình như Hình 62.
bạn nga muốn xếp bốn hình tròn giống nhau có bán kính 3 cm như hình vẽ tính độ dài cạnh mảnh bìa đó bạn mai cần dùng để vừa đủ xếp bốn hình tròn đó
a) Mỗi hình sau có mấy góc?
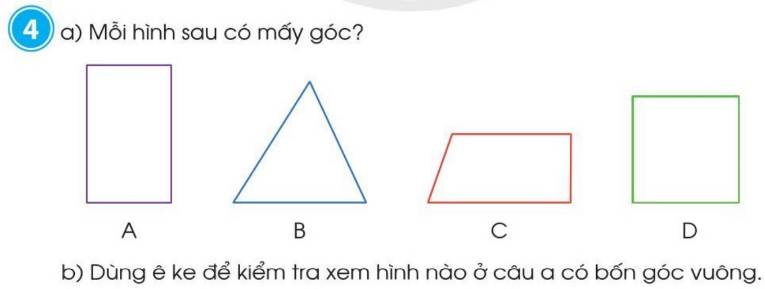
b) Dùng ê ke để kiểm tra xem hình nào ở câu a có bốn góc vuông.
`a,`
Hình `A:` có `4` góc
Hình `B:` có `3` góc
Hình `C:` có `4` góc
Hình `D:` có `4` góc
`b,` Hình `A, D` có `4` góc vuông
Tự làm ê ke giấy: Gấp tờ giấy làm đôi, rồi lại gấp làm đôi tiếp (như hình vẽ).
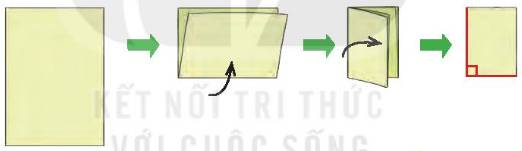
a) Dùng ê ke trong bộ đồ dùng học tập của em, hãy kiểm tra lại góc vuông ở ê ke giấy vừa làm.
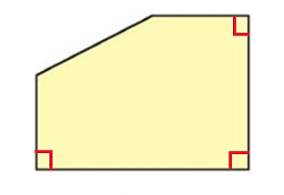
b) Dùng ê ke giấy vừa làm, em hãy tìm trong hình bên có mấy góc vuông.
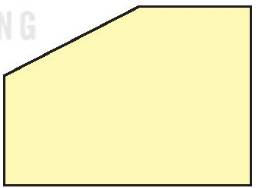
a) Gấp hình theo yêu cầu bài toán sau đó kiểm tra em thấy các góc vừa gấp được là các góc vuông.
b) Trong hình bên có 3 góc vuông. Đó là các góc như hình vẽ sau:
Huy chơi trò xếp 36 que tăm thành những hình giống nhau như dưới đây. Trong mỗi trường hợp a, b, c, d, Huy xếp được bao nhiêu hình như vậy?
a) Mỗi hình cần 3 que diêm
Huy xếp được: 36 : 3 = 12 hình
b) Mỗi hình cần 4 que diêm
Huy xếp được: 36 : 4 = 9 hình
c) Mỗi hình cần 9 que diêm
Huy xếp được 36 : 9 = 4 hình
d) Mỗi hình cần 12 que diêm
Huy xếp được: 36 : 12 = 3 hình.
"Bàn làm việc đa năng: Hãy cắt 6 hình thang cân giống nhau rồi ghép thành hình mặt chiếc bàn làm việc như hình dưới đây:
từ 18 hình lập phương giống hệt nhau, có bao nhiêu cách xếp để thành hình hộp chữ nhật?
18 = 1x18 = 2x9 = 3x6
Vậy số cách xếp bằng các tích 2 số tự nhiên trên
Coi mỗi cạnh của hình lập phương là 1 đơn vị khi đó thể tích của 18 hình lập phương là:
(1\(\times\)1 \(\times\) 1)\(\times\) 18 = 18 ( đơn vị thể tích)
Thể tích của hình hộp chữ nhật được xếp thành từ 18 hình lập phương nhỏ là : 18 ( đơn vị thể tích)
Vì: 1 \(\times\) 1 \(\times\) 18 = 18; 1 \(\times\) 2 \(\times\) 9 = 18 ; 1 \(\times\) 3 \(\times\) 6 = 18
2 \(\times\) 3 \(\times\) 3 = 18;
trường hợp : 1 \(\times\)1 \(\times\)18 = 18 ta có hình hộp chữ nhật có các kích thước dài, rộng cao là: ( 1; 1; 18); ( 18; 1; 1 ) có 2 cách xếp
Trường hợp 1 \(\times\) 2 \(\times\) 9 ta có hình hộp chữ nhật có các kích thước dài, rộng, cao là: (2; 1; 9); (9; 1; 2); ( 9; 2; 1) có 3 cách xếp.
Trường hợp 1 \(\times\) 3 \(\times\) 6 = 18 ta có hình hộp chữ nhật có các kích thước dài, rộng, cao: (3; 1; 6); ( 6; 1; 3); ( 6; 3; 1) có 3 cách xếp
Trường hợp 2 \(\times\) 3 \(\times\) 3 = 18 ta có hình hộp chữ nhật có các kích thước dài, rộng, cao lần lượt là: (3; 2; 3); ( 3; 3; 2) có 2 cách xếp.
Số cách sắp xếp hình chữ nhật là:
2 + 3 + 3 + 2 = 10 ( cách)
Đáp số: 10 cách.
Bạn Trang lấy 4 que tính dài bằng nhau xếp thành hình 4 cạnh như Hình 3. Bạn ấy nói rằng đó là hình vuông. Em hãy dùng thước và êke để kiểm tra xem bạn Trang nói như vậy đúng hay sai.
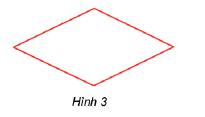
Sử dụng êke đo góc và thấy 4 góc không vuông nên đây không là hình vuông.
Vậy bạn Trang nói sai.
Cho hình thoi ABCD. Hai đường chéo AC và BD của hình thoi cắt nhau tại điểm O.
Dùng ê ke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không.
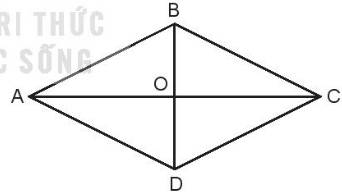
Hai đường chéo AC và BD vuông góc với nhau.
Từ một tấm tôn hình vuông có cạnh 8dm, bác Hùng cắt bỏ bốn phần như nhau ở bốn góc, sau đó bác hàn các mép lại để được một chiếc thùng (không có nắp) như Hình 7.99.
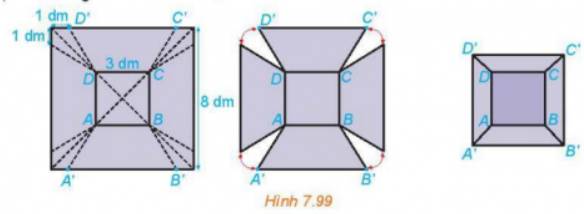
a) Giải thích vì sao chiếc thùng có dạng hình chóp cụt.
b) Tính cạnh bên của thùng.
c) Hỏi thùng có thể chứa được nhiều nhất bao nhiêu lít nước?
a) AB // A’B’ \( \Rightarrow \) AB // (A’B’C’D’), AD // A’D’ \( \Rightarrow \) AD // (A’B’C’D’)
Do đó (ABCD) // (A’B’C’D’).
Chiếc thùng có dạng hình chóp cụt vì khi bác Hùng cắt bỏ bốn phần như nhau ở bốn góc của tấm tôn vuông, sẽ tạo thành bốn tam giác vuông cân.
Vậy chiếc thùng có dạng hình chóp cụt.
b) Cạnh bên của hình chóp cụt bằng \(\sqrt {\frac{9}{4} + \frac{{25}}{4}} = \frac{{\sqrt {34} }}{2}\left( {dm} \right)\)
c) Xét mặt chứa đường chéo của hình vuông, nó là hình thang cân có chiều cao bằng chiều cao của hình chóp cụt và được \(h = \sqrt {\frac{{34}}{4} - \frac{{18}}{4}} = 2\left( {dm} \right)\)
Thể tích cần tìm là V = 42 lít.
Cho bốn hình tam giác như hình bên :
a) Hãy xếp bốn hình tam giác đó thành một hình dưới đây :