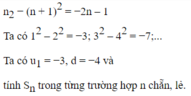\(=\left(1-2\right)\left(1+2\right)+\left(3-4\right)\left(3+4\right)+...+\left(2003-2004\right)\left(2003+2004\right)+2005^2\\ =-\left(1+2\right)-\left(3+4\right)-...-\left(2003+2004\right)+2005^2\\ =-\left(1+2+3+...+2003+2004\right)+2005^2\\ =-\dfrac{\left(2004+1\right)\cdot2004}{2}+2005^2\\ =2011015\)

a) có tất cả số hạng là:

(20042-12):10+1=2004

tổng là:

\(\dfrac{\text{(20042+12).2004}}{2}\)\(=20094108\)

Ta có \(2^2+4^2+...+20^2=2^2\left(1^2+2^2+...+10^2\right)=2^2.385=1540\).

S = 22 + 42 + 62 + ... + 202

   = (2.1)2 + (2.2)2 + (2.3)2 ... (2.10)2

   = 22.12 + 22.22 + 22.32 + ... + 22.102

   = 22 (12 + 22 + ... + 102 )

   = 4 . 385 = 1540

Ta có : \(1^2+2^2+3^2+.....+10^2=385\)

\(\Leftrightarrow2^2\left(1^2+2^2+3^2+.....+10^2\right)=2^2.385\)

\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=4.385\)

\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=1540\)

Sửa đề: CHo 1²+2²+...+10²=385. Tính S = 2²+4² +...+ 20²

S = 2² + 4² +...+ 20²

= (1.2)² + (2.2)² +...+ (2.10)²

= 1².2² + 2².2² +...+ 2².10²

= 2²(1² + 2² +...+ 10²)

= 4.385

= 1540

S= 1^2  .  2^2 + 2^2 . 2^2  + ... + 10^2 . 2^2
  = 4. ( 1^2 + 2^2 +...+ 10^2)  = 4 . 385 = 1540

chúc bạn học giỏi

42-(2x+32)+12:2=6

42-2x-32+6=6

=> 42-32-2x=0

=> 10-2x=0

=>2x=10=> x=5

cái tính tổng thì theo công thức tính tổng: số đầu+số cuối)x số số hạng:2

số số hạng:(497-2):5+1=100

tổng là: 499x100:2

\(1,42-\left(2x+32\right)+12:2=6\)

\(\Rightarrow42-2x-32=0\)

\(\Rightarrow10-2x=0\)

\(\Rightarrow2x=10\Leftrightarrow x=5\)

\(2,S=2+7+12+17+...+497\)

\(\Rightarrow S=\frac{\left(497+2\right)\left[\left(497-2\right):5+1\right]}{2}\)

\(\Rightarrow S=\frac{499.100}{2}=499.50\)

\(\Rightarrow S=24950\)

D) 42 - (2x + 32 ) + 12 : 2 = 6

42 - (2x + 32 ) + 12 = 6 . 2

42 - ( 2x + 32 ) + 12 = 12

42 - (2x + 32 ) = 12 - 12

42 - (2x + 32) = 0

2x + 32 = 42 - 0

2x +32 = 42

2x = 42 - 32

2x = 10

x = 10 : 2

x = 5

Vậy x = 5

Tính tổng :

S = 2 + 7 + 12 + 17 + 22 +....+ 492 + 497

= ( 497 - 2 ) : 5 + 1 

= 100

= (2 + 497 ) . 100 : 2

= 24 950

Vậy S = 24 950

=-5+(-5)+(-5)+(-5)

=-5x4=-20

\(2003^2-3^2=\left(2003-3\right)\left(2003+3\right)=2000.2006=4012000\)

\(2003^2-3^2=\left(2003-3\right)\left(2003+3\right)=2000\cdot2006=2\cdot1000\cdot2006=4012000\)

a.

$S=1+2+2^2+2^3+...+2^{2017}$
$2S=2+2^2+2^3+2^4+...+2^{2018}$

$\Rightarrow 2S-S=(2+2^2+2^3+2^4+...+2^{2018}) - (1+2+2^2+2^3+...+2^{2017})$

$\Rightarrow S=2^{2018}-1$

b.

$S=3+3^2+3^3+...+3^{2017}$
$3S=3^2+3^3+3^4+...+3^{2018}$

$\Rightarrow 3S-S=(3^2+3^3+3^4+...+3^{2018})-(3+3^2+3^3+...+3^{2017})$

$\Rightarrow 2S=3^{2018}-3$
$\Rightarrow S=\frac{3^{2018}-3}{2}$
 

Câu c, d bạn làm tương tự a,b. 

c. Nhân S với 4. Kết quả: $S=\frac{4^{2018}-4}{3}$

d. Nhân S với 5. Kết quả: $S=\frac{5^{2018}-5}{4}$