CMR : 2016/ căn 2017 + 2017/ căn 2016 > căn 2017 + căn 2016

Những câu hỏi liên quan
chứng minh căn 2016 - 2* căn 2017 + căn 2018 < 0
cần CM: \(\sqrt{2018}+\sqrt{2016}< \)\(2\sqrt{2017}\)
<=> \(2018+2016+2\sqrt{2018\cdot2016}< \)\(4\cdot17\)
<=>\(\sqrt{2018\cdot2016}< \)\(17\)
<=>\(\sqrt{2017^2-1}\)\(< \sqrt{2017^2}\) (BĐT luôn đúng)
Do đó \(\sqrt{2016}-2\sqrt{2017}+\sqrt{2018}< 0\)
Đúng 0
Bình luận (0)
So sánh(không dùng bảng số hoặc máy tính)
a)căn 5+căn 7 và căn 13
b)16 và căn 15 . căn 17
c)căn 2015+căn 2017 và 2.căn 2016
c) Bình phương hai vế ta được 2015+2017+2\(\sqrt{2015\times2017}\) và 4\(\times\)2016
Ta có 2015 + 2017 + 2\(\sqrt{2015\times2017}\)
= (2016-1) + (2016+1) + 2\(\sqrt{2015\times2017}\)
= 2016 + 2016 + 1 - 1 + 2\(\sqrt{2015\times2017}\)
= 2\(\times\)2016 + 2\(\sqrt{2015\times2017}\) (1)
ta thấy 2015 \(\times\) 2017 =(2016-1) \(\times\) (2016+1)= 20162 - 1
nên (1) \(\Leftrightarrow\)2\(\times\)2016 + 2\(\sqrt{2016^2-1}\)
Ta có 4\(\times\)2016=2\(\times\)2016 + 2\(\times\)2016=2\(\times\)2016 + 2\(\sqrt{2016^2}\)
Vì 20162-1 < 20162 nên 2\(\sqrt{2016^2-1}\) < 2\(\sqrt{2016^2}\)
\(\Leftrightarrow\) 2\(\times\)2016 + 2\(\sqrt{2016^2-1}\) < 2\(\times\)2016 + 2\(\sqrt{2016^2}\)
\(\Leftrightarrow\)2015+2017+2\(\sqrt{2015\times2017}\) < 4\(\times\)2016
Hay \(\sqrt{2015}+\sqrt{2017}\) < \(2\sqrt{2016}\)
Đúng 1
Bình luận (0)
a) Bình phương hai vế ta được 5+7+\(2\sqrt{5\times7}\) và 13.
Ta có 5+7+\(2\sqrt{5\times7}\) =12+\(2\sqrt{35}\)
13=12+1=12+\(2\times\frac{1}{2}\) =12+\(2\sqrt{\frac{1}{4}}\)
Vì 35 > \(\frac{1}{4}\) nên \(\sqrt{35}\) > \(\sqrt{\frac{1}{4}}\) \(\Leftrightarrow\)2\(\sqrt{35}\) > \(2\sqrt{\frac{1}{4}}\) \(\Leftrightarrow\)12+2\(\sqrt{35}\) > 12+\(2\sqrt{\frac{1}{4}}\)
Hay\(\sqrt{5}\)+\(\sqrt{7}\) > \(\sqrt{13}\)
Đúng 0
Bình luận (2)
b) Bình phương hai vế ta được 162 và 15\(\times\)17
Ta có 15\(\times\)17=(16-1)\(\times\)(16+1)=162-1 < 162
\(\Leftrightarrow\)162 > 15\(\times\)17 Hay \(\sqrt{16}>\sqrt{15}\times\sqrt{17}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm GTNN
P= 2017+ căn bậc x-2018
Q= 2x-3\5-3x ( x thuộc Z)
Tìm GTLN
B= x+2 \|x| ) x thuộc Z)
C= 2016* x -1 \ 2015*x+2016
2017/căn 2018+2018/căn 2017 so sánh với căn 2017 + căn 2018
Áp dụng BĐT Svác-xơ ta có:
\(\frac{2017}{\sqrt{2018}}+\frac{2018}{\sqrt{2017}}\ge\frac{\left(\sqrt{2017}+\sqrt{2018}\right)^2}{\sqrt{2017}+\sqrt{2018}}=\sqrt{2017}+\sqrt{2018}\)
do \(\frac{2017}{\sqrt{2018}}\ne\frac{2018}{\sqrt{2017}}\)nên dấu "=" không xảy ra
Vậy \(\frac{2017}{\sqrt{2018}}+\frac{2018}{\sqrt{2017}}>\sqrt{2017}+\sqrt{2018}\)
Đúng 0
Bình luận (0)
Tìm x biết:
\(\sqrt{17+\sqrt{17+\sqrt{17+...+\sqrt{17}}}}\). x = 1 + 2 + 3 +...+ 2016 + 2017
( 12 dấu căn )
Ta có: \(1+2+3+...+n=\frac{n\left(n+1\right)}{2}\)
\(\Rightarrow VP=\frac{2017\left(2017+1\right)}{2}=2035153\)
Lại có:\(VT^2=17+\sqrt{17+\sqrt{17+...+\sqrt{17}}}\)
\(\Rightarrow VT^2-VT=17\Rightarrow VT^2-VT-17=0\)
\(\Rightarrow VT=\frac{\sqrt{69}+1}{2}>0\) (thỏa)
\(\frac{\sqrt{69}+1}{2}x=2035153\Rightarrow x=...\)
Có gì đó sai sai
Đúng 0
Bình luận (0)
Ra x= 437355,8081 :(
Chả biết đúng hay sai
Mà giải thích chỗ \(\frac{\sqrt{69}+1}{2}\)được không?
Đúng 0
Bình luận (0)
\(VT^2-VT-17=0\)
\(\Delta=\left(-1\right)^2-4\cdot\left(-17\right)=69\)
\(\Rightarrow VT_{1,2}=\frac{1\pm\sqrt{69}}{2}\Rightarrow VT=\frac{1+\sqrt{69}}{2}\) vì VT>0
Đúng 0
Bình luận (0)
Cho biểu thức:
\(A=\frac{3-\sqrt{3+\sqrt{3+\sqrt{3+...+\sqrt{3}}}}}{6-\sqrt{3+\sqrt{3+\sqrt{3+....+\sqrt{3}}}}}\)
Tử có 2017 dấu căn, mẫu có 2016 dấu căn. Chứng minh \(A< \frac{1}{4}\)
Cho biểu đồ:DIỆN TÍCH VÀ DÂN SỐ CỦA MỘT SỐ QUỐC GIA NĂM 2016 (Nguồn số liệu theo Niên giám thống kê Việt Nam 2017, NXB Thống kê, 2018) Căn cứ vào biểu đồ trên, cho biết nhận xét nào sau đây không đúng và của một số quốc gia năm 2016? A. Diện tích lãnh thổ của Cam-pu-chia thấp nhất trong ba nước B. Số dân của Việt Nam cao hơn Cam-pu-chia và thấp hơn Thái Lan C. Tổng số dân của Cam-pu-chia và Thái Lan thấp hơn số dân của Việt Nam D. Diện tích lãnh thổ của Thái Lan lớn hơn diện tích lãnh thổ củ...
Đọc tiếp
Cho biểu đồ:
DIỆN TÍCH VÀ DÂN SỐ CỦA MỘT SỐ QUỐC GIA NĂM 2016
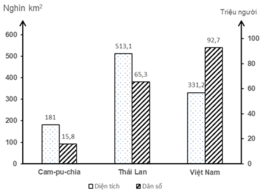
(Nguồn số liệu theo Niên giám thống kê Việt Nam 2017, NXB Thống kê, 2018)
Căn cứ vào biểu đồ trên, cho biết nhận xét nào sau đây không đúng và của một số quốc gia năm 2016?
A. Diện tích lãnh thổ của Cam-pu-chia thấp nhất trong ba nước
B. Số dân của Việt Nam cao hơn Cam-pu-chia và thấp hơn Thái Lan
C. Tổng số dân của Cam-pu-chia và Thái Lan thấp hơn số dân của Việt Nam
D. Diện tích lãnh thổ của Thái Lan lớn hơn diện tích lãnh thổ của Việt Nam
Đáp án B
Biểu đồ cho thấy Việt Nam có số dân lớn nhất trong ba nước, cao hơn Thái Lan và Cam-pu-chia. (92,7 triệu người > 65,5 và 15,8 triệu người)
=> Nhận xét Việt Nam có số dân cao hơn Cam-pu-chia và thấp hơn Thái Lan là không đúng.
Đúng 0
Bình luận (0)
Cho biểu đồ: DIỆN TÍCH VÀ DÂN SỐ CỦA MỘT SỐ QUỐC GIA NĂM 2016 (Nguồn số liệu theo Niên giám thống kê Việt Nam 2017, NXB Thống kê, 2018) Căn cứ vào biểu đồ trên, cho biết nhận xét nào sau đây không đúng và của một số quốc gia năm 2016? A. Diện tích lãnh thổ của Cam-pu-chia thấp nhất trong ba nước B. Số dân của Việt Nam cao hơn Cam-pu-chia và thấp hơn Thái Lan C. Tổng số dân của Cam-pu-chia và Thái Lan thấp hơn số dân của Việt Nam D. Diện tích lãnh thổ của Thái Lan lớn hơn diện tích lãnh thổ c...
Đọc tiếp
Cho biểu đồ: DIỆN TÍCH VÀ DÂN SỐ CỦA MỘT SỐ QUỐC GIA NĂM 2016

(Nguồn số liệu theo Niên giám thống kê Việt Nam 2017, NXB Thống kê, 2018)
Căn cứ vào biểu đồ trên, cho biết nhận xét nào sau đây không đúng và của một số quốc gia năm 2016?
A. Diện tích lãnh thổ của Cam-pu-chia thấp nhất trong ba nước
B. Số dân của Việt Nam cao hơn Cam-pu-chia và thấp hơn Thái Lan
C. Tổng số dân của Cam-pu-chia và Thái Lan thấp hơn số dân của Việt Nam
D. Diện tích lãnh thổ của Thái Lan lớn hơn diện tích lãnh thổ của Việt Nam
Đáp án B
Biểu đồ cho thấy Việt Nam có số dân lớn nhất trong ba nước, cao hơn Thái Lan và Cam-pu-chia. (92,7 triệu người > 65,5 và 15,8 triệu người)
=> Nhận xét Việt Nam có số dân cao hơn Cam-pu-chia và thấp hơn Thái Lan là không đúng
Đúng 0
Bình luận (0)
Cho biểu đồ:(Nguồn: Niên giám thống kê Việt Nam 2016, NXB Thống kê, Hà Nội, 2017)Căn vào biểu đồ, cho biết nhận xét nào sau đây đúng về sản lượng than và điện của Trung Quốc giai đoạn 2012 - 2015? A. Sản lượng than tăng, sản lượng điện giảm B. Sản lượng than giảm, sản lượng điện tăng C. Sản lượng than và điện đều giảm. D. Sản lượng than và điện đều tăng
Đọc tiếp
Cho biểu đồ:

(Nguồn: Niên giám thống kê Việt Nam 2016, NXB Thống kê, Hà Nội, 2017)
Căn vào biểu đồ, cho biết nhận xét nào sau đây đúng về sản lượng than và điện của Trung Quốc giai đoạn 2012 - 2015?
A. Sản lượng than tăng, sản lượng điện giảm
B. Sản lượng than giảm, sản lượng điện tăng
C. Sản lượng than và điện đều giảm.
D. Sản lượng than và điện đều tăng















